SpheroidalEigenvalue

SpheroidalEigenvalue[n,m,γ]

gives the spheroidal eigenvalue with degree and order .

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • The spheroidal eigenvalues for successive 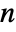correspond to the successive values of 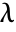for which there exist normalizable solutions to the differential equation .
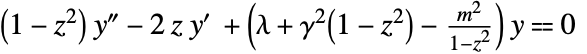  • SpheroidalEigenvalue[n,m,0]is equal to .
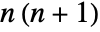  • For certain special arguments, SpheroidalEigenvalue automatically evaluates to exact values.
  • SpheroidalEigenvalue can be evaluated to arbitrary numerical precision.
  • SpheroidalEigenvalue automatically threads over lists. »

Examples

open allclose all

Basic Examples  (4)

Evaluate numerically:

Plot over a subset of the reals:

Series expansion in the spherical limit as γ approaches 0:

Series expansion at Infinity:

Scope  (14)

Numerical Evaluation  (5)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number inputs:

Evaluate efficiently at high precision:

Compute the elementwise values of an array using automatic threading:

Or compute the matrix SpheroidalEigenvalue function using MatrixFunction:

Specific Values  (7)

Simple exact values are generated automatically:

Evaluate symbolically for integer parameters:

Evaluate symbolically for half-integer parameters:

Find the maximum of SpheroidalEigenvalue[1,2/3,x]:

SpheroidalEigenvalue evaluates exactly if m=1 and γ=n π/2:

SpheroidalEigenvalue threads elementwise over lists:

TraditionalForm formatting:

Visualization  (2)

Plot the SpheroidalEigenvalue function for integer orders:

Plot the real part of TemplateBox[{2, 1, {x, +, {i, , y}}}, SpheroidalEigenvalue]:

Plot the imaginary part of TemplateBox[{2, 1, {x, +, {i, , y}}}, SpheroidalEigenvalue]:

Applications  (3)

Solve the spheroidal differential equation:

Solve this spheroidal-type differential equation:

Find a branch point of SpheroidalEigenvalue:

Properties & Relations  (1)

For half-integer values, the SpheroidalEigenvalue reduces to the MathieuCharacteristicA function:

Possible Issues  (1)

SpheroidalEigenvalue does not evaluate for half-integer or for generic :

The half-integer values of are singular for the near-spherical expansion:

Wolfram Research (2007), SpheroidalEigenvalue, Wolfram Language function, https://reference.wolfram.com/language/ref/SpheroidalEigenvalue.html.

Text

Wolfram Research (2007), SpheroidalEigenvalue, Wolfram Language function, https://reference.wolfram.com/language/ref/SpheroidalEigenvalue.html.

CMS

Wolfram Language. 2007. "SpheroidalEigenvalue." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SpheroidalEigenvalue.html.

APA

Wolfram Language. (2007). SpheroidalEigenvalue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SpheroidalEigenvalue.html

BibTeX

@misc{reference.wolfram_2024_spheroidaleigenvalue, author="Wolfram Research", title="{SpheroidalEigenvalue}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/SpheroidalEigenvalue.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_spheroidaleigenvalue, organization={Wolfram Research}, title={SpheroidalEigenvalue}, year={2007}, url={https://reference.wolfram.com/language/ref/SpheroidalEigenvalue.html}, note=[Accessed: 21-December-2024 ]}