Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Wolfram Language & System Documentation Center

SpheroidalPS

SpheroidalPS

SpheroidalPS[n,m,γ,z]

gives the angular spheroidal function of the first kind.

Details

Mathematical function, suitable for both symbolic and numerical manipulation.
The angular spheroidal functions satisfy the differential equation 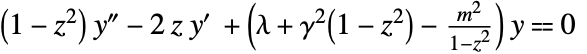with the spheroidal eigenvalue 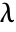given by SpheroidalEigenvalue[n,m,γ].
SpheroidalPS[n,m,0,z] is equivalent to LegendreP[n,m,z].
SpheroidalPS[n,m,a,γ,z] gives spheroidal functions of type 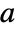. The types are specified as for LegendreP.
For certain special arguments, SpheroidalPS automatically evaluates to exact values.
SpheroidalPS can be evaluated to arbitrary numerical precision.
SpheroidalPS automatically threads over lists. »

Examples

open all close all

Basic Examples (6)

Evaluate numerically:

Expansion about the spherical case:

Plot over a subset of the reals:

Series expansion at the origin:

Series expansion at Infinity:

Series expansion at a singular point:

Scope (25)

Numerical Evaluation (6)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number inputs:

Evaluate efficiently at high precision:

Compute the elementwise values of an array using automatic threading:

Or compute the matrix SpheroidalPS function using MatrixFunction:

Compute average-case statistical intervals using Around:

Specific Values (4)

Evaluate symbolically:

Find the first positive minimum of SpheroidalPS[4,0,1/2,x]:

Evaluate the SpheroidalPS function for half-integer parameters:

Different SpheroidalPS types give different symbolic forms:

Visualization (3)

Plot the SpheroidalPS function for various orders:

Plot the real part of :

Plot the imaginary part of :

Types 2 and 3 of SpheroidalPS functions have different branch cut structures:

Function Properties (8)

The real domain of :

The complex domain of :

is an even function with respect to :

has the mirror property :

has no singularities or discontinuities:

is neither non-decreasing nor non-increasing:

is not injective:

is neither non-negative nor non-positive:

TraditionalForm formatting:

Differentiation (2)

The first derivative with respect to z:

Higher derivatives with respect to z:

Plot the higher derivatives with respect to z when n=10, m=2 and γ=1/3:

Series Expansions (2)

Find the Taylor expansion using Series:

Plots of the first three approximations around :

The Taylor expansion at a generic point:

Generalizations & Extensions (1)

The different types of SpheroidalPS have different branch cut structures:

Applications (4)

Solve the spheroidal differential equation in terms of SpheroidalPS:

Plot prolate and oblate versions of the same angular function:

SpheroidalPS is a band-limited function with bandwidth proportional to :

For spheroidicity parameter :

For spheroidicity parameter , the bandwidth is higher:

Build a near-spherical approximation to :

First few terms of the approximation:

Compare numerically:

Properties & Relations (1)

Spheroidal angular harmonics are eigenfunctions of the Sinc transform on the interval :

Possible Issues (2)

Spheroidal functions do not evaluate for half-integer values of or generic values of :

Angular spheroidal harmonics in the Wolfram Language adopt the Meixner–Schaefke normalization scheme:

Flammer normalization is also common:

Reconstruct table entries from Abramowitz and Stegun table 21.2:

Top