Surd
Surd[x,n]
gives the real-valued ![]()
![]() root of x.
root of x.
Details

- Surd[x,n] returns the real-valued
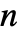
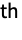 root of real-valued x for odd n.
root of real-valued x for odd n. - Surd[x,n] returns the principal
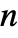
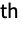 root for non-negative real-valued x and even n.
root for non-negative real-valued x and even n. - For symbolic x in Surd[x,n], x is assumed to be real valued.
- Surd can be evaluated to arbitrary numerical precision.
- Surd automatically threads over lists. »
- In StandardForm, Surd[x,n] formats as
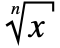 .
.  can be entered as
can be entered as  surd
surd , and
, and  moves between the fields.
moves between the fields.- Surd can be used with Interval and CenteredInterval objects. »
Examples
open allclose allBasic Examples (5)
Scope (31)
Numerical Evaluation (5)
The precision of the output tracks the precision of the input:
Evaluate efficiently at high precision:
Compute the elementwise values of an array using automatic threading:
Or compute the matrix Surd function using MatrixFunction:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Specific Values (4)
Visualization (4)
Plot the Surd function for various orders:
Visualize the absolute value and argument (sign) of ![]() for odd n:
for odd n:
The function ![]() has the same absolute value but a different argument for
has the same absolute value but a different argument for ![]() :
:
Function Properties (8)
Surd[x,n] is defined for all real x when n is a positive, odd integer:
For positive, even n, it is defined for non-negative x:
For negative n, 0 is removed from the domain:
Surd is not defined for nonreal complex values:
Surd[x,n] achieves all non-negative real values when n is a positive even integer:
For positive odd n, its range is the whole real line:
For negative n, 0 is removed from the range:
Surd[x,n] is not an analytic function of x for any integer n:
Decreasing for negative even ![]() :
:
And it is surjective onto ![]() for odd, positive
for odd, positive ![]() , but not other values of
, but not other values of ![]() :
:
It is non-negative on its real domain for even ![]() :
:
![]() in general has both singularities and discontinuities at zero:
in general has both singularities and discontinuities at zero:
However, for positive odd ![]() it is continuous at the origin:
it is continuous at the origin:
![]() is neither convex nor concave for odd
is neither convex nor concave for odd ![]() :
:
On its domain of definition, it is concave for positive even ![]() and convex of negative even
and convex of negative even ![]() :
:
Differentiation (3)
Integration (3)
Compute the indefinite integral using Integrate:
Series Expansions (4)
Find the Taylor expansion using Series:
Plots of the first three approximations around ![]() :
:
General term in the series expansion using SeriesCoefficient:
Applications (1)
With ![]() , the real vector field corresponding to the complex function
, the real vector field corresponding to the complex function ![]() is
is ![]() , and the trajectories that follow the field satisfy the differential equation
, and the trajectories that follow the field satisfy the differential equation ![]() . The implicit solution is
. The implicit solution is ![]() for real
for real ![]() , which corresponds to a family of circles that are tangent to the real axis at the origin:
, which corresponds to a family of circles that are tangent to the real axis at the origin:
In polar coordinates, the trajectories are ![]() for any real
for any real ![]() :
:
More generally, for ![]() where
where ![]() is an integer, the streamlines follow
is an integer, the streamlines follow ![]() for constant
for constant ![]() :
:
This also works for negative powers:
For odd powers, care must be taken to ensure the first argument to Surd is non-negative:
Properties & Relations (3)
Possible Issues (1)
Neat Examples (1)
Plot a composition of Surd:
Text
Wolfram Research (2012), Surd, Wolfram Language function, https://reference.wolfram.com/language/ref/Surd.html.
CMS
Wolfram Language. 2012. "Surd." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Surd.html.
APA
Wolfram Language. (2012). Surd. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Surd.html