SystemsModelSeriesConnect[sys1,sys2]
connects systems models sys1 and sys2 in series.
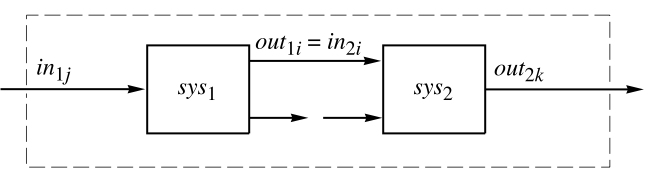
SystemsModelSeriesConnect[sys1,sys2,{{out11,in21},…}]
connects outputs out1i of sys1 to inputs in2i of sys2.


SystemsModelSeriesConnect
SystemsModelSeriesConnect[sys1,sys2]
connects systems models sys1 and sys2 in series.
SystemsModelSeriesConnect[sys1,sys2,{{out11,in21},…}]
connects outputs out1i of sys1 to inputs in2i of sys2.
Details
- The systems model sysi can be a TransferFunctionModel, StateSpaceModel, AffineStateSpaceModel, or NonlinearStateSpaceModel.
- The inputs and outputs of the system produced by SystemsModelSeriesConnect are the inputs of sys1 and the outputs of sys2, respectively.
- The arguments in1i and out1i are integers specifying the positions of the input or output channels.
Examples
open all close allBasic Examples (4)
Scope (13)
Basic Uses (5)
Connect multivariable systems:
Connect the second output from the first system to the first input of the second system:
Connect discrete-time systems:
Connect a StateSpaceModel to a TransferFunctionModel:
System Types (8)
Connect two TransferFunctionModel systems:
Using improper transfer functions:
Connect two StateSpaceModel systems:
Using descriptor state-space models:
Input linear AffineStateSpaceModel systems:
General nonlinear NonlinearStateSpaceModel systems:
Connecting a transfer function and a state-space model will give a state-space model:
Reversing the order gives an equivalent state-space model:
They give the same transfer functions:
Connecting a standard linear system and an input linear system will give an affine model:
Connecting a linear or affine system with a nonlinear system gives a nonlinear model:
Applications (4)
A function that connects any number of matching systems in series:
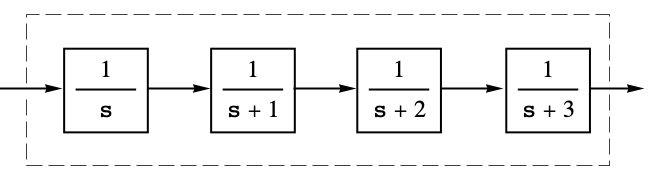
Connect a family of first-order systems in series:
Connect several multiple-input, multiple-output systems:
The cascade of four abstract systems:
The tree structure of the cascade:
Create a positioning system with a power amplifier, motor, and angular rate sensor in series:
Visualize the open-loop step response:
Integrate the last output of a three-output system:
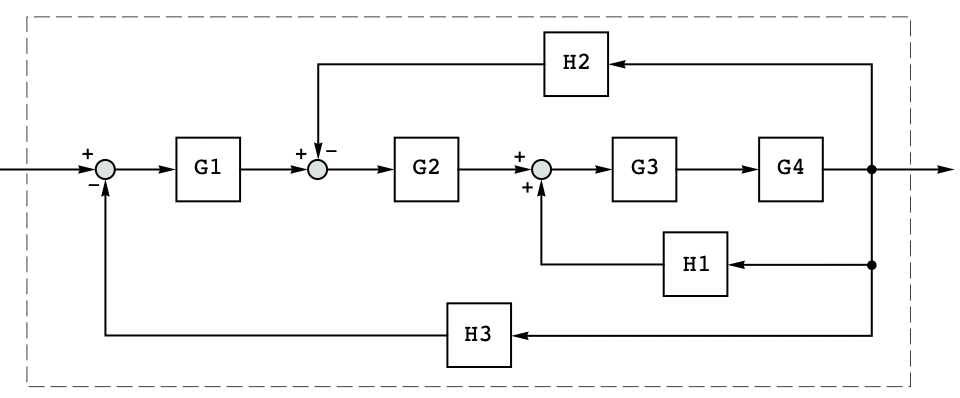
Use SystemsModelSeriesConnect in multi-loop reduction:
Properties & Relations (8)
The resulting system has the inputs of the first system and the outputs of the second system:
SystemsModelSeriesConnect is a special case of SystemsConnectionsModel:
SystemsModelSeriesConnect does not cancel poles and zeros:
A system made from series and parallel connections has the same poles as the subsystems:
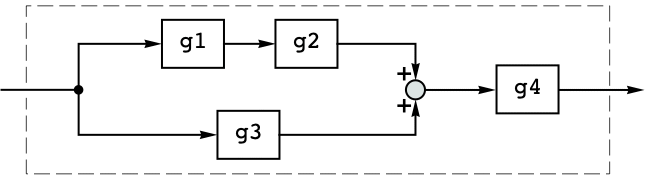
They're the same as the poles of its individual components:
The order of the reduced system is the sum of the orders of the subsystems:
The connected system has an order of 4:
It is the sum of the individual model orders:
SystemsModelSeriesConnect is essentially a flat function:
Series connections are equivalent to multiplication without any pole-zero cancellation:
The series connection of two models is the convolution of their impulse responses:
Text
Wolfram Research (2010), SystemsModelSeriesConnect, Wolfram Language function, https://reference.wolfram.com/language/ref/SystemsModelSeriesConnect.html (updated 2014).
CMS
Wolfram Language. 2010. "SystemsModelSeriesConnect." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/SystemsModelSeriesConnect.html.
APA
Wolfram Language. (2010). SystemsModelSeriesConnect. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SystemsModelSeriesConnect.html
BibTeX
@misc{reference.wolfram_2025_systemsmodelseriesconnect, author="Wolfram Research", title="{SystemsModelSeriesConnect}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/SystemsModelSeriesConnect.html}", note=[Accessed: 11-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_systemsmodelseriesconnect, organization={Wolfram Research}, title={SystemsModelSeriesConnect}, year={2014}, url={https://reference.wolfram.com/language/ref/SystemsModelSeriesConnect.html}, note=[Accessed: 11-January-2026]}