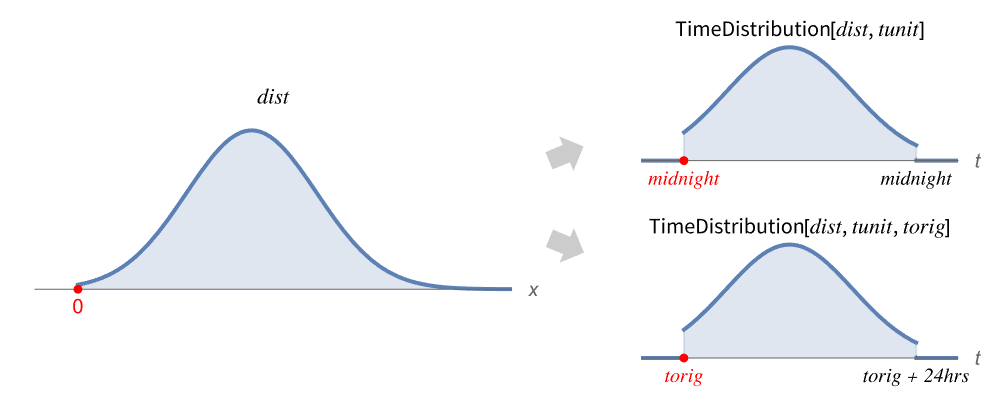
TimeDistribution[dist,tunit]
represents a linear distribution of time of day according to dist with time scale unit tunit originating at midnight.
TimeDistribution[dist, tunit, torig]
represents a linear distribution of time of day with time origin at torig.


TimeDistribution
TimeDistribution[dist,tunit]
represents a linear distribution of time of day according to dist with time scale unit tunit originating at midnight.
TimeDistribution[dist, tunit, torig]
represents a linear distribution of time of day with time origin at torig.
Details and Options

- TimeDistribution works by rescaling the distribution dist to the space of quantities with the unit tunit, truncating to the length of the day, and then mapping to the space of times, where the numeric origin becomes the time origin torig.
- For a continuous distribution dist, the DateGranularity is taken to be "Instant". »
- For a discrete distribution dist, the DateGranularity is given by tunit. »
- The distribution dist can be any univariate distribution that satisfies DistributionParameterQ. »
- The date scale unit tunit should be a time unit as returned by UnitDimensions[dscale]. »
- The date origin torig should be a TimeObject.
- TimeDistribution[dist,tunit] is equivalent to TimeDistribution[dist,tunit,TimeObject[0]].
- Sampling from TimeDistribution gives TimeObject.
- TimeDistribution can used in functions such as RandomVariate, Mean, ....
Examples
open all close allBasic Examples (2)
Scope (6)
Define a continuous time distribution with mean at noon:
Compute the mean of the distribution:
Simulate a list of times and visualize their distribution:
Define a nonsymmetric distribution of times starting at 8am:
Estimate TimeDistribution from the collection of times:
Since the data histogram is bell shaped, fit a normal distribution to the data:
Compute distribution functions:
The number of patients arriving at an emergency room has been recorded for each hour from 1am to midnight:
Create a nonparametric model of the data:
Options (1)
Time Zone (1)
Specifying TimeZone will override the date origin input:
Properties & Relations (3)
Extract properties of a TimeDistribution:
Granularity of a discrete time distribution is given by the date scale unit:
Granularity of a continuous time distribution is always "Instant":
Possible Issues (2)
The input distribution must be a valid distribution:
Check if a distribution is valid:
The unit must be a valid time unit:
Check if a unit is a time unit:
Or use KnownUnitQ with the second argument set to "Time":
Related Guides
History
Text
Wolfram Research (2024), TimeDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/TimeDistribution.html.
CMS
Wolfram Language. 2024. "TimeDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TimeDistribution.html.
APA
Wolfram Language. (2024). TimeDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TimeDistribution.html
BibTeX
@misc{reference.wolfram_2025_timedistribution, author="Wolfram Research", title="{TimeDistribution}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/TimeDistribution.html}", note=[Accessed: 11-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_timedistribution, organization={Wolfram Research}, title={TimeDistribution}, year={2024}, url={https://reference.wolfram.com/language/ref/TimeDistribution.html}, note=[Accessed: 11-March-2026]}