TimeSeriesForecast

TimeSeriesForecast[tproc,data,k]

gives the k-step-ahead forecast beyond data according to the time series process tproc.

TimeSeriesForecast[tsmod,k]

gives the k-step-ahead forecast for TimeSeriesModel tsmod.

Details and Options

  • TimeSeriesForecast[tproc,{x0,…,xm},k] will give Expectation[x[m+k]x[0]x0∧…∧x[m]xm], where xtproc, the expected value of the process given data.
  • TimeSeriesForecast allows tproc to be a time series process such as ARProcess, ARMAProcess, SARIMAProcess, etc.
  • The data can be a list of numeric values {x1,x2,…}, a list of time-value pairs {{t1,x1},{t2,x2},…}, or TemporalData.
  • The following forecast specifications can be given:
  • kat the k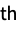^(th) step ahead
    {kmax}at 1, …, kmax steps ahead
    {kmin,kmax}at kmin, …, kmax steps ahead
    {{k1,k2,…}}use explicit {k1,k2,…} steps ahead
  • TimeSeriesForecast returns the forecasted value if k is an integer and TemporalData otherwise.
  • The default for k is 1.
  • TimeSeriesForecast supports a Method option with the following settings:
  • Automaticautomatically determine the method
    "AR"approximate with a large-order AR process
    "Covariance"exact covariance function-based
    "Kalman"use Kalman filter
  • The mean squared errors of the prediction are the compounded noise errors and are given as MetaInformation in the TemporalData output. For forecast=TimeSeriesForecast[tproc,data,k], the mean squared errors can be accessed by forecast["MeanSquaredErrors"].

Examples

open allclose all

Basic Examples  (3)

Forecast three steps ahead for an ARProcess:

An ARMAProcess:

Predict the seventh value from TimeSeriesModel:

Mean squared error of the forecast:

Forecast a vector-valued time series process:

Find the forecast for the next 10 steps:

Plot the data and the forecast for each component:

Scope  (7)

Step  (4)

Forecast one step ahead:

Forecast the third step ahead:

Find forecast for all the steps ahead up to the fifth:

Show the path:

Forecast all the steps ahead in the range from third to fifth:

Show the path:

Forecast for a list of steps:

Path:

Mean Squared Errors  (3)

Forecast one step ahead:

Return the forecast as TemporalData to extract mean squared errors:

Find the forecast with mean squared errors:

Calculate the forecast:

Standard errors:

Define the error bands:

Plot the data and forecast with mean error bands:

Find the forecast with 95% confidence intervals:

Find the forecast for the next 10 steps:

Find mean squared errors and confidence intervals:

Plot data, forecast, and the forecast limits:

Options  (4)

Method  (4)

Find the forecast using the covariance-based method:

Find the forecast using the autoregressive method:

Find the forecast using the Kalman filter method:

Compare exact and approximate methods for an MAProcess:

Both methods agree for the autoregressive processes:

Applications  (3)

The daily exchange rates of the euro to the dollar from May 2012 through September 2012:

Fit an AR process to the exchange rates:

Forecast for 20 business days ahead:

Plot the forecast with original data:

Consider hourly temperature readings for September 9, 2012, near your location:

The data contains missing values:

Redefine time series with MissingDataMethod to fill in missing data with interpolated values:

Check if the time stamps are regularly spaced:

Resample by an hour:

Estimate an ARProcess:

Calculate prediction for the next 12 hours:

Plot forecast with original data:

Retail monthly sales in United States:

Create TimeSeries from the selection:

Plot the sales with grid lines at December peaks:

Fit a seasonal model:

The process parameters:

Find forecast for the next 7 years:

Calculate 95% confidence bands for the forecast:

There is an upper and a lower band:

Plot the forecast within the 95% confidence region:

Properties & Relations  (3)

Forecasting with ARProcess using the exact or approximate method gives the same result:

Forecast is the same for a time series process and its invertible representation:

This process is not invertible:

Find its invertible representation:

Compare forecasts:

Use TimeSeriesModel to forecast:

Compute forecast for 20 steps:

Use process and data explicitly:

Compare paths:

Possible Issues  (2)

"Kalman" method requires the parameters of the process to be numeric:

If the invertible representation does not exist, the forecast may not be reliable:

Wolfram Research (2012), TimeSeriesForecast, Wolfram Language function, https://reference.wolfram.com/language/ref/TimeSeriesForecast.html (updated 2014).

Text

Wolfram Research (2012), TimeSeriesForecast, Wolfram Language function, https://reference.wolfram.com/language/ref/TimeSeriesForecast.html (updated 2014).

CMS

Wolfram Language. 2012. "TimeSeriesForecast." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/TimeSeriesForecast.html.

APA

Wolfram Language. (2012). TimeSeriesForecast. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TimeSeriesForecast.html

BibTeX

@misc{reference.wolfram_2024_timeseriesforecast, author="Wolfram Research", title="{TimeSeriesForecast}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/TimeSeriesForecast.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_timeseriesforecast, organization={Wolfram Research}, title={TimeSeriesForecast}, year={2014}, url={https://reference.wolfram.com/language/ref/TimeSeriesForecast.html}, note=[Accessed: 17-November-2024 ]}