TimeSeriesModelFit
TimeSeriesModelFit[data]
自動的に選択されたモデル族から data のための時系列モデルを構築する.
TimeSeriesModelFit[data,mspec]
mspec で指定されたモデル族から data のための時系列モデルを構築する.
詳細とオプション




- 時系列の解析にはTimeSeriesModelFitが使われる.これは,可能なモデルの大規模なクラスから時系列モデルを自動的に選択する.
- TimeSeriesModelFitは,構築する時系列モデルを表す記号的TimeSeriesModelオブジェクトを返す.モデルの特性と診断は model[property]から得ることができる.
- model["Properties"]を使って使用可能なモデル特性のリストを得ることができる.
- data は,数値のリスト{x1,x2,…},時間と値のペアのリスト{{t1,x1},{t2,x2},…},TimeSeries,あるいはTemporalDataである.
- 時間 t におけるモデルの値は model[t]で得ることができる.t が入力データの範囲にある場合は,時間 t におけるデータが返される.その他の場合は予測値が与えられる.
- 時間 t における予測限界は,model["PredictionLimits"][t]で得ることができる.
- モデル指定 mspec は次の形を取ることができる.
-
Automatic 使用するモデルを自動的に選択する "family" 指定された族からモデルを選択する {"family",params} 指定された族の部分集合からモデルを選択する - 次の族とパラメータ化を使うことができる.
-
"AR" {p} 自己回帰モデル族 "MA" {q} 移動平均モデル族 "ARMA" {p,q} 自己回帰移動平均モデル族 "ARIMA" {p,d,q} 和分ARMAモデル族 "SARMA" {{p,q},{sp,sq},s} 季節ARMAモデル族 "SARIMA" {{p,d,q},{sp,sd,sq},s} 季節ARIMAモデル族 "ARCH" {q} ARCHモデル族 "GARCH" {q,p} GARCHモデル族 - 自己回帰次数および移動平均次数の p および q,またそれらに季節性を与えた sp および sq は,Automatic,非負の整数,非負の整数のリスト,そのようなリストを示すSpanのいずれかで与えることができる.
- 非季節型の和分次数および季節型の和分次数の d および sd は,Automatic,非負の整数,非負の整数のリスト,そのようなリストを示すSpanのいずれかで与えることができる.
- 季節モデルについては,季節母数 s はAutomaticあるいは正の整数でよい.
- 追加的なモデル族のパラメータ化は,例題で示してある.
- model["property"]を使って次のモデル特性を得ることができる.
-
"BestFit" フィットされたモデル "BestFitParameters" 係数推定 "ErrorVariance" モデルの誤差分散 "FitResiduals" フィットされたモデルの残差 "StandardizedResiduals" 標準化されたモデル残差 "TemporalData" データをTemporalDataとして入力する - モデル選択に関連する特性
-
"CandidateModels" 選択基準で分類された候補モデルの集合 "CandidateModelSelectionValues" 各候補モデルのための選択基準の値 "CandidateSelectionTable" モデルと選択基準の値を含む表 "CandidateSelectionTableEntries" 候補選択表からの項目 "ModelFamily" 選択されたモデル族 "SelectionCriterion" 最適なモデルの選択に使用された基準 - 適合度を測る特性
-
"AIC" 赤池情報量基準 "AICc" 有限サンプル修正AIC "BIC" ベイズ(Bayes)情報量基準 "SBC" シュワルツ(Schwartz)–ベイズ情報量基準 - 次の特性を使ってモデル残差の白色性を査定することができる.
-
"ACFPlot" 残差の自己相関のプロット "ACFValues" "ACFPlot"からの値 "PACFPlot" 残差の偏自己相関のプロット "PACFValues" "PACFPlot"からの値 "LjungBoxPlot" Ljung–Box残差自己相関検定の 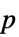 値のプロット
値のプロット"LjungBoxValues" "LjungBoxPlot"からの値 - 残差の白色特性"wprop"のために含める遅れの最大数は,model["wprop","LagMax"->max]を与えることで制御することができる.ただし,max は正の整数である.
- 係数推定のための特性と診断
-
"CovarianceMatrix" モデル係数のための共分散推定 "InformationMatrix" モデル係数のための情報行列 "ParameterConfidenceIntervals" 係数推定についての信頼区間 "ParameterStandardErrors" モデル係数の標準誤差 "ParameterTable" フィットされた係数情報の表 "ParameterTableEntries" 母数表の項目 - TimeSeriesModelFitは次のオプションを取る.
-
ConfidenceLevel 95/100 選択する信頼水準 IncludeConstantBasis Automatic モデル中に定数を含めるかどうか Method Automatic モデルの選択に使用するメソッド WorkingPrecision Automatic 内部計算の精度 - デフォルト設定のIncludeConstantBasis->Automaticは,非季節型の和分次数と季節型の和分次数の両方が0のときは,モデル中に定数を含む.その他の場合は定数は含まれない.
- Method->m 中のメソッド m は"Stepwise"または"GridSearch"である.段階的選択の場合,最適な選択基準のモデルが求まるまで,Automaticの母数次数は徐々に増大する.グリッド検索を使うと,指定されたグリッド上のすべてのモデルが余すことなく試される.
- 最高のモデルは,選択基準 crit に従って選ばれる.この基準はMethod->{m,"SelectionCriterion"->crit}で設定することができる.有効な選択基準には,"AIC"(デフォルト),"AICc","SBC","BIC"等がある.
例題
すべて開くすべて閉じるスコープ (22)
基本的な用法 (5)
もとのデータを使って,TimeSeriesModelでの将来的な観測のシミュレーションを行う:
最もフィットする過程を使って,将来的な観測のシミュレーションを10回行う:
タイムスタンプあるいは初期値についての情報は,RandomFunctionには全く渡されていない:
もとのデータによって与えられた情報を使うために,TimeSeriesModelを使ってシミュレーションを行う:
モデル指定 (6)
モデル特性 (11)
同等に,Normalを使う:
選ばれたモデルについて,いくつかのフィッティングの基準を示す:
"ACFPlot"に使われた,最初の5個の自己相関値および95%信頼区間:
"PACFPlot"に使われた,最初の5個の偏自己相関値および95%信頼区間:
オプション (9)
ConfidenceLevel (2)
WorkingPrecision (1)
WorkingPrecisionを使ってより高精度の推定を得る:
アプリケーション (8)
航空機の乗客 (2)
素数 (1)
事故死 (1)
オオヤマネコの皮 (1)
小売り (1)
選択したものからTimeSeriesを作る:
医薬品販売と広告 (1)
次の時系列は,アメリカ合衆国の特許医薬品所有者であるLydia Pinkhamの,半年ごとの売上げと広告費である.Pinkham氏は家庭薬としてVegetable Compoundの製造を開始し,近所の人に配った.彼女の作った化合物は,薬草の粉末で,アルコールが18%含まれていた.Pinkham一族は1875年に,この,神経衰弱から子宮脱まであらゆる女性症状を治すという薬品を市場に売り出すことを決めた.この薬品は急速に支持を得,間もなく売上げが年間30万ドル近くにまでなった.薬品と公告に関する国の規制が厳しくなった1920年代になって,Lydia E. Pinkham Medicine Coは薬品のアルコール分を減らし,謳う効用も控えめにした:
考えられる問題 (2)
次のデータは,月ごとにサンプリングされ,季節性12を持つとことが分かっている:
TemporalDataは,このデータが月ごとに等間隔で置かれていることは分かっていない:
28日という最小時間増分で自動リサンプリングを行うと,季節性が13になる:
TemporalDataがデータを規則性を持つものとして扱うようにする:
TimeSeriesModelFitは,モーメント法を使って候補となる過程の母数を推定する.異なる推定器を用いると順位が変わることがある:
テキスト
Wolfram Research (2014), TimeSeriesModelFit, Wolfram言語関数, https://reference.wolfram.com/language/ref/TimeSeriesModelFit.html.
CMS
Wolfram Language. 2014. "TimeSeriesModelFit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TimeSeriesModelFit.html.
APA
Wolfram Language. (2014). TimeSeriesModelFit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TimeSeriesModelFit.html