UnitRootTest[data]
tests whether data came from an autoregressive time series process with unit root.
UnitRootTest[data,model,"property"]
returns the value of "property" for a given model.


UnitRootTest
UnitRootTest[data]
tests whether data came from an autoregressive time series process with unit root.
UnitRootTest[data,model,"property"]
returns the value of "property" for a given model.
Details and Options



- UnitRootTest performs a hypothesis test on the time series data with the null hypothesis
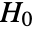 that the time series satisfying an AR model has a unit root in the denominator of the corresponding transfer function and the alternative hypothesis
that the time series satisfying an AR model has a unit root in the denominator of the corresponding transfer function and the alternative hypothesis 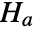 that it does not.
that it does not. - Rejecting the null hypothesis allows the conclusion that the detrended data could have come from a stationary time series.
- By default, a probability value or
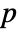 -value is returned.
-value is returned. - A small
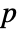 -value suggests that the presence of a unit root is unlikely.
-value suggests that the presence of a unit root is unlikely. - The data can be a list of values {x1,x2,…,xn} or a TemporalData object.
- The model allows the specification of a model
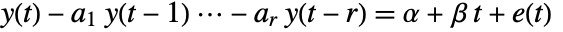 , where
, where 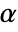 is the constant offset,
is the constant offset, 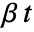 is a linear drift, and
is a linear drift, and 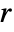 is the order of the AR model.
is the order of the AR model. - The following model specifications can be used:
-
Automatic 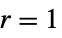 and
and 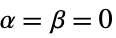
r 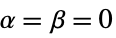
"Constant" 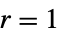 and
and 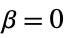
"Drift" 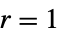
{"Constant",r} 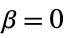
{"Drift", r} general case - UnitRootTest[data] will choose Dickey–Fuller F test with
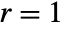 and
and 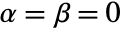 .
. - UnitRootTest[data,model,All] will choose all tests that apply to data and model.
- UnitRootTest[data,model,"test"] reports the
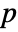 -value according to "test".
-value according to "test". - The following tests can be used:
-
"DickeyFullerF" based on 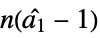
"DickeyFullerT" based on 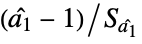
"PhillipsPerronF" adjusted Dickey–Fuller F test "PhillipsPerronT" adjusted Dickey–Fuller T test - UnitRootTest[data,model,"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
- UnitRootTest[data,model,"property"] can be used to directly give the value of "property".
- Properties related to the reporting of test results include:
-
"AllTests" list of all applicable tests "AutomaticTest" test chosen if Automatic is used "PValue" list of 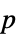 -values
-values"PValueTable" formatted table of 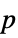 -values
-values"ShortTestConclusion" a short description of the conclusion of a test "TestConclusion" a description of the conclusion of a test "TestData" list of pairs of test statistics and 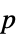 -values
-values"TestDataTable" formatted table of 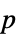 -values and test statistics
-values and test statistics"TestStatistic" list of test statistics "TestStatisticTable" formatted table of test statistics - The following option can be used:
-
SignificanceLevel 0.05 cutoff for diagnostics and reporting - For unit root tests, a cutoff
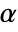 is chosen such that
is chosen such that 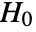 is rejected only if
is rejected only if 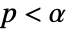 . The value of
. The value of 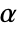 used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. By default,
used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. By default, 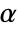 is set to 0.05.
is set to 0.05.
Examples
open all close allBasic Examples (1)
Scope (17)
Testing (13)
Test time series data for a unit root:
The ![]() -values are typically large when a unit root is present:
-values are typically large when a unit root is present:
The ![]() -values are typically small when a unit root is not present:
-values are typically small when a unit root is not present:
Test for unit root with null hypothesis that the underlying model is ARProcess[2]:
Setting the model to Automatic is equivalent to assuming an underlying ARProcess[1]:
Test for unit root, accounting for an underlying nonzero mean:
Account for a nonzero mean and assume an underlying ARProcess[3]:
Assume a nonzero mean and deterministic trend:
Assume a nonzero mean, deterministic trend, and an underlying ARProcess[3]:
Perform a particular test for unit root:
Any number of tests can be performed simultaneously:
Using Automatic applies the Dickey–Fuller F test:
The property "AutomaticTest" can be used to determine which test was chosen:
Perform all tests appropriate to the data simultaneously:
Use the property "AllTests" to identify which tests were used:
Create a HypothesisTestData object for repeated property extraction:
The properties available for extraction:
Extract some properties from the HypothesisTestData object:
The ![]() -value and test statistic from the "DickeyFullerT" test:
-value and test statistic from the "DickeyFullerT" test:
Reporting (4)
Tabulate the results from a selection of tests:
A full table of all appropriate test results:
A table of selected test results:
Retrieve the entries from a test table for customized reporting:
The ![]() -values are above 0.05, so there is not enough evidence to reject
-values are above 0.05, so there is not enough evidence to reject ![]() at that level:
at that level:
Tabulate ![]() -values for a test or group of tests:
-values for a test or group of tests:
A table of ![]() -values from all appropriate tests:
-values from all appropriate tests:
A table of ![]() -values from a subset of tests:
-values from a subset of tests:
Report the test statistic from a test or group of tests:
Options (1)
Applications (3)
Maximum daily rainfall data for a 47-year period in Sydney, Australia was recorded. Of interest is whether a simple autoregressive model can model this data:
The data obviously has nonzero mean:
Choose the order of the underlying ARProcess using Schwert's rule of thumb:
There is evidence of a unit root, suggesting a simple ARProcess is not an adequate model:
Consider the annual revenue (in millions) by commercial airlines in the United States from 1937 to 1960:
The trend is confirmed using UnitRootTest:
Removing the linear trend appears to be sufficient:
Fit an ARIMAProcess to the time series:
Forecast revenue 10 years ahead using the fitted model:
Use a unit root test to determine trend presence:
Possible Issues (2)
The Phillips–Perron tests are limited to ARProcess[1] models:
Use Dickey–Fuller type tests to test higher orders:
UnitRootTest fails for irregularly sampled data:

Or set TemporalRegularity to be true:
Neat Examples (2)
Related Guides
History
Text
Wolfram Research (2012), UnitRootTest, Wolfram Language function, https://reference.wolfram.com/language/ref/UnitRootTest.html.
CMS
Wolfram Language. 2012. "UnitRootTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/UnitRootTest.html.
APA
Wolfram Language. (2012). UnitRootTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/UnitRootTest.html
BibTeX
@misc{reference.wolfram_2025_unitroottest, author="Wolfram Research", title="{UnitRootTest}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/UnitRootTest.html}", note=[Accessed: 29-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_unitroottest, organization={Wolfram Research}, title={UnitRootTest}, year={2012}, url={https://reference.wolfram.com/language/ref/UnitRootTest.html}, note=[Accessed: 29-December-2025]}