TimeSeriesModelFit

TimeSeriesModelFit[data]

从自动选择的模型系列中构建 data 的时间序列模型.

TimeSeriesModelFit[data,mspec]

从由 mspec 指定的模型系列中构建 data 的时间序列.

更多信息和选项

  • TimeSeriesModelFit 用于时间序列分析. 它从一大类可能的模型中自动选择时间序列模型.
  • TimeSeriesModelFit 返回符号 TimeSeriesModel 对象，表示它构建的时间序列模型. 模型的属性和诊断可以从 model[property] 中获得.
  • 可以使用 model["Properties"] 获得可用模型属性列表.
  • data 可以是数值 {x1,x2,…} 的列表，时间-值对 {{t1,x1},{t2,x2},…} 的列表，一个 TimeSeries 或 TemporalData.
  • 在时间 t 的模型值可以通过给定 model[t] 获得. 如果 t 在输入数据的范围，那么会返回在时间 t 的数据；否则会给出预测值.
  • 在时间 t 的预报预测极限可以使用 model["PredictionLimits"][t] 获得.
  • 模型规范 mspec 可以采取以下形式：
  • Automatic自动选择要使用的模型
    "family"从给定系列中选择一个模型
    {"family",params}从给定系列的子集中选择一个模型
  • 可以使用以下系列和参数：
  • "AR"{p}自回归模型系列
    "MA"{q}移动平均模型系列
    "ARMA"{p,q}自回归移动平均模型系列
    "ARIMA"{p,d,q}整合 ARMA 模型系列
    "SARMA"{{p,q},{sp,sq},s}季节性 ARMA 模型系列
    "SARIMA"{{p,d,q},{sp,sd,sq},s}季节性 ARIMA 模型系列
    "ARCH"{q}ARCH 模型系列
    "GARCH"{q,p}GARCH 模型系列
  • 自回归和移动平均阶数 p 和 q 以及它们的季节性的相对物 sp 和 sq 可被赋值为 Automatic、非负整数、非负整数列表或一个 Span 表示的这样的一份列表.
  • 非季节和季节积分阶数 d 和 sd 可被赋值为 Automatic、非负整数、非负整数列表或一个 Span 表示的这样的一份列表.
  • 对于季节性模型，季节参数 s 可以是 Automatic 或一个正整数.
  • 其他模型系列参数在范例中给出.
  • 下列模型属性可用 model["property"] 获得：
  • "BestFit"拟合模型
    "BestFitParameters"系数估计
    "ErrorVariance"模型误差方差
    "FitResiduals"拟合模型的残差
    "StandardizedResiduals"标准化模型的残差
    "TemporalData"作为 TemporalData 的输入数据
  • 与模型选择有关的属性包括：
  • "CandidateModels"按选择标准排序的候选模型集合
    "CandidateModelSelectionValues"每个候选模型的选择标准值
    "CandidateSelectionTable"包含模型和选择标准值的表格
    "CandidateSelectionTableEntries"候选选择表格的条目
    "ModelFamily"选择的模型系列
    "SelectionCriterion"选择最好模型的标准
  • 衡量拟合优度的属性包括：
  • "AIC"Akaike 信息量准则
    "AICc"有限样本修正的 AIC
    "BIC"Bayesian 信息量准则
    "SBC"Schwartz–Bayes 信息量准则
  • 以下属性可用于估计模型残差的白噪声：
  • "ACFPlot"残差自相关的图线
    "ACFValues""ACFPlot" 的值
    "PACFPlot"残差偏自相关的图线
    "PACFValues""PACFPlot" 的值
    "LjungBoxPlot"Ljung–Box 残差自相关检验 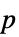值的图线
    "LjungBoxValues""LjungBoxPlot" 的值
  • 残差白噪声属性 "wprop" 包括的最大滞后数通过 model["wprop","LagMax"->max] 进行控制，其中 max 是正整数.
  • 系数估计的属性和诊断包括：
  • "CovarianceMatrix"模型系数的协方差估计
    "InformationMatrix"模型系数的信息矩阵
    "ParameterConfidenceIntervals"系数估计的置信区间
    "ParameterStandardErrors"模型系数的标准误差
    "ParameterTable"拟合系数信息表格
    "ParameterTableEntries"参数表格中的条目
  • TimeSeriesModelFit 采用以下选项：
  • ConfidenceLevel 95/100要选择的置信区间
    IncludeConstantBasis Automatic是否在模型中包含常数
    Method Automatic模型选择使用的方法
    WorkingPrecision Automatic内部计算中使用的精确度
  • 如果非季节性和季节性积分阶数为零，默认设置 IncludeConstantBasis->Automatic 会在模型中包含一个常数；否则的话，不会包含常数.
  • Method->m 中的方法 m 可以是 "Stepwise" 或 "GridSearch". 对于逐步选择，Automatic 参数阶数递增直到找到一个最优化的选择标准. 使用网格搜索在指定网格彻底尝试所有模型.
  • 根据选择标准 crit 选择最佳模型，它可以在 Method->{m,"SelectionCriterion"->crit} 中设置. 有效的选择标准范例包括 "AIC"（默认）、"AICc"、"SBC" 和 "BIC".

范例

打开所有单元关闭所有单元

基本范例  (1)

对一些数据拟合时间序列模型：

拟合的时间序列模型：

在时间35获取点预测和95%预测极限：

用10步向前预测可视化数据：

范围  (22)

基本用途  (5)

自动拟合一个模型为时间序列：

为数据选择的模型：

使用某些月温度数据创建预测：

月温度数据和24个月预测：

预测2014年6月1号的平均温度：

预测的95%置信区间：

拟合一个特殊模型为时间序列：

用一个 "GARCH"(1,1) 模型拟合数据：

模型和参数估计：

用一个时间序列模型拟合一个100个工作日的时间序列：

模拟下一个30个工作日50次：

使用原始数据用 TimeSeriesModel 模拟未来观察：

拟合一个模型：

使用最佳拟合过程模拟10个未来观察：

时间戳或初始值的信息不会传给 RandomFunction：

使用 TimeSeriesModel 的模拟会使用由原始数据给出的信息：

模型规范  (6)

为时间序列自动选择模型：

等价于指定 Automatic：

找到在特殊系列中的模型：

搜索模型的自回归系列：

从一个明确的候选集中选择最佳模型：

搜索 ARMA 系列，其中，阶数 和 为0到2：

用固定阶数拟合模型：

用 "ARIMA"(2,1,3) 模型拟合数据：

拟合积分阶数并搜索自回归和移动平均阶数：

参数化模型的 ARIMA 系列：

自动检测阶数 、 和 ：

或者，对所有参数阶数使用 Automatic：

相同的方法，固定积分阶数 ，其中， 和 为 Automatic：

相同的方法，固定 和 ，其中设积分阶数 为 Automatic：

参数化模型的 SARIMA 系列：

自动检测 、、、、、 和 ：

或者，对所有参数阶数使用 Automatic：

同样，固定季节性参数 ，其他为 Automatic：

同样，固定季节性参数 ，积分阶数 和 ：

模型属性  (11)

获取可用属性列表：

提取最佳拟合过程：

使用 Normal 得到同等的结果：

显示选择模型的某些拟合标准：

用于选择最佳模型的标准：

报告能拟合数据的前几个模型：

表格中的条目：

获取拟合数据的候选模型列表：

通过 AIC 比较模型：

检验拟合残差是否自相关：

在滞后3时有一个明显的尖峰：

添加平均移动成分去除滞后3的自相关：

检验拟合残差的偏相关函数是否为0：

在滞后3有明显的尖峰：

添加移动平均成分去除在滞后3的偏相关：

检验模型残差的自相关：

在滞后3和4有明显的尖峰：

添加移动平均成分去除明显的自相关：

获取用在残差白噪声诊断图中使用的值：

在 "ACFPlot" 中使用了前5个自相关值和95%的置信区域：

在 "PACFPlot" 中使用了前5个偏自相关值和95%的置信区域：

滞后1到12的 Ljung–Box 值和标准值被用在图线中：

报告模型参数的值和显著性：

来自于表格的值：

从参数协方差矩阵中获取参数标准误差：

可以直接获取标准误差：

选项  (9)

ConfidenceLevel  (2)

为预测极限设置置信水平：

使用90%的置信水平：

拟合后置信水平可以更改：

ConfidenceLevel 设置影响特征检测的阈值：

IncludeConstantBasis  (1)

需要为模型估计常数：

设置常数为0：

Method  (5)

默认情况下，使用逐步搜索选择参数阶数：

使用网格搜索：

执行混合搜索：

使用不同的选择标准选取最佳模型：

默认情况下，使用 "AIC"：

使用 "BIC"：

设置候选模型的最大数目，以便继续报告：

保留最多15个模型：

保留所有适合的模型：

默认情况下，保留10个模型：

设置最大允许的自回归和移动平均阶数：

最大阶数限制拟合的模型数目：

逐步方法拟合模型在当前最佳模型的 "MaxStepSize" 阶数中：

默认情况下，最大阶数步长设为1：

增加步长大小可以提高质量，但是可能增加搜索时间：

比较网格搜索：

WorkingPrecision  (1)

使用 WorkingPrecision 获取更高精度的估计：

应用  (8)

本地温度  (1)

预测在你的位置，下一个月的平均温度：

过去10年本地平均月温度：

拟合时间序列模型：

下一个月的预测：

在95%的置信带中绘制明年的预测：

飞机上的乘客  (2)

以下数据包括1949年1月到1960年12月美国国际航空乘客（按千计）的月总人数：

在1958年1月分割数据：

对1958年前的飞机乘客数据拟合一个时间序列模型：

比较1959年6月预测的和实际的飞机乘客数：

1958年到1961年预测数据与实际数据比较：

模拟未来7年的飞机乘客数并和预测相比较：

对数据进行时间序列模型拟合：

创建7年预报并预测极限：

绘制预测的图线：

模拟未来7年的100条路径：

显示带有模拟路径的95%预测极限：

质数  (1)

对实际和估计的质数间的不同拟合一个时间序列模型：

调整模型到差异：

显示带有95%预测极限的下一个100个不同的预测：

使用模型改善对第300个质数的估计：

原始的和改进的估计与实际质数相比：

意外死亡  (1)

美国的意外死亡数按月记录了6年：

对数据进行 ARProcess 拟合：

该模型忽略了数据的季节性：

诊断图建议需要一个带有12个季节性的模型：

季节性模型似乎普遍比非季节性的好：

获取未来2个月的90%预报预测极限的经验估计：

比较渐进估计：

山猫毛皮  (1)

加拿大哈德逊湾公司在1850年到1911年每年销售的水貂皮草数：

对数据拟合模型：

模拟下一个10年的模型的值：

模拟的值可能是负的，但是平均函数提供正的预测：

绘制由模拟给出的预测的数据：

零售销售  (1)

美国每月的零售销售额：

根据选择创建 TimeSeries：

在12月尖峰时用网格线绘制销售额：

拟合季节性模型：

过程参数：

找到下一个7年的参数：

计算预测的95%置信带：

有上下带：

在95%的置信区域内绘制预测：

医药销售和广告  (1)

以下的时间序列是美国医药专利所有人丽迪亚·平克汉姆的双季度的销售和广告. 平克汉姆开始制作蔬菜合剂作为家庭药物，并与她的邻居共享. 她的合剂是磨碎的药草混合，含有18%的酒精. 1875年平克汉姆家庭决定从商卖药，她声称她的药可医治从神经衰弱到子宫下垂的任何妇女疾病. 很快就获得认可，一年净收入将近39万美元. 直到20世纪20年代，当联邦药品和广告法规增加时，Lydia E. Pinkham Medicine Co. 同时降低医药的酒精含量和其疗效的声明：

为数据找到模型：

预测下一个5年的值：

该模型预测客户对平克汉姆药物疗效的信赖的急剧下降：

可能存在的问题  (2)

以下数据是每月的样本，并且季节性参数为 12：

TemporalData 不知道数据是按月等间隔的：

按 28 天的最小时间增量自动重采样会导致季节参数变为 13：

告诉 TemporalData 对数据按常规处理：

没有必要重新采样；季节性参数被保留：

TimeSeriesModelFit 使用时刻方法估计候选过程的参数. 不同估计器的使用会导致不同的排名：

2阶最大似然性估计：

最大似然估计被每个选择标准所使用：

Wolfram Research (2014)，TimeSeriesModelFit，Wolfram 语言函数，https://reference.wolfram.com/language/ref/TimeSeriesModelFit.html.

文本

Wolfram Research (2014)，TimeSeriesModelFit，Wolfram 语言函数，https://reference.wolfram.com/language/ref/TimeSeriesModelFit.html.

CMS

Wolfram 语言. 2014. "TimeSeriesModelFit." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/TimeSeriesModelFit.html.

APA

Wolfram 语言. (2014). TimeSeriesModelFit. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TimeSeriesModelFit.html 年

BibTeX

@misc{reference.wolfram_2024_timeseriesmodelfit, author="Wolfram Research", title="{TimeSeriesModelFit}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/TimeSeriesModelFit.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_timeseriesmodelfit, organization={Wolfram Research}, title={TimeSeriesModelFit}, year={2014}, url={https://reference.wolfram.com/language/ref/TimeSeriesModelFit.html}, note=[Accessed: 21-November-2024 ]}