TransferFunctionModel
TransferFunctionModel[g[s],s]
複素変数 s を持つ伝達関数行列 g[s]のモデルを表す.
TransferFunctionModel[{n[s],d[s]},s]
伝達関数モデルの分子 n[s] と分母 d[s] を指定する.
TransferFunctionModel[{z,p,g},s]
伝達関数モデルの零点 z,極 p,ゲインg を指定する.
系のモデル sys の伝達関数モデルを与える.
詳細とオプション

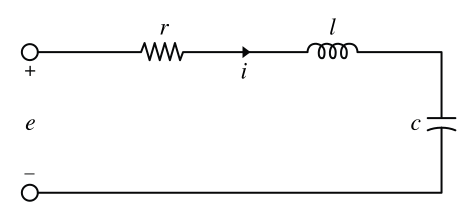
- TransferFunctionModelは,通常,信号フィルタおよび制御設計に使われる.
 でモデル化される連続時間系(ただし,
でモデル化される連続時間系(ただし,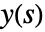 は出力のラプラス変換,
は出力のラプラス変換,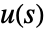 は入力のラプラス変換,
は入力のラプラス変換,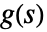 は伝達行列)はTransferFunctionModel[g[s],s]として指定できる.
は伝達行列)はTransferFunctionModel[g[s],s]として指定できる.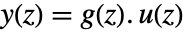 でモデル化される離散時間系(ただし,
でモデル化される離散時間系(ただし,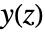 は出力のZ変換,
は出力のZ変換,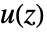 は丹入力のZ変換,
は丹入力のZ変換,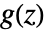 は伝達行列)は,TransferFunctionModel[g[z],z,SamplingPeriodτ]として指定できる.
は伝達行列)は,TransferFunctionModel[g[z],z,SamplingPeriodτ]として指定できる.- SystemsModelDelayを使って,任意の伝達関数モデルに時間遅延を含ませることができる.
- TransferFunctionModel[sys]は,次の系を変換することができる.
-
AffineStateSpaceModel 近似テイラー(Taylor)変換 NonlinearStateSpaceModel 近似テイラー変換 StateSpaceModel 厳密変換 - 使用可能なオプション
-
Method Automatic 状態空間モデルの伝達関数を求めるためのメソッド SamplingPeriod Automatic 系のサンプリング周期 SystemsModelLabels Automatic 入出力変数のラベル ExternalTypeSignature Automatic 埋め込まれたコードの変数型 - Methodオプションの設定値には"DeterminantExpansion","ResolventIdentities","Inverse","Generic"等がある.Method->Automaticとすると,伝達関数モデルは行列式の展開を使って計算される.
例題
すべて開くすべて閉じる例 (5)
スコープ (19)
AffineStateSpaceModelにテイラー線形化を施し,その伝達関数表現を得る:
非零の平衡値を使ったAffineStateSpaceModelの線形化:
NonlinearStateSpaceModelのテイラー線形化:
オプション (5)
特性と関係 (8)
TransferFunctionModelは引数が1つの純関数として動作する:
TransferFunctionFactorを使って因子分解された形を得る:
TransferFunctionCancelを使って共通の極と零点を相殺する:
考えられる問題 (3)
TransferFunctionModel[m,var]では,極零点ペアは処理される前に相殺されることがある:
Unevaluatedを使って相殺を防ぐ:
あるいはTransferFunctionModel[{num,den},var]を使って:
あるいはTransferFunctionModel[{z,p,g},var]を使って:
TransferFunctionModel[m,var]では結果がより高次の系になる可能性がある:
あるいはTransferFunctionModelに渡す前に m を簡約する:
複素変数 var が指定されていない場合,それは連続時間系ではsであると解釈される:
テキスト
Wolfram Research (2010), TransferFunctionModel, Wolfram言語関数, https://reference.wolfram.com/language/ref/TransferFunctionModel.html (2014年に更新).
CMS
Wolfram Language. 2010. "TransferFunctionModel." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/TransferFunctionModel.html.
APA
Wolfram Language. (2010). TransferFunctionModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TransferFunctionModel.html