TransferFunctionModel[g[s],s]
表示具有复数变量 s 的传递函数矩阵 g[s] 的模型.
TransferFunctionModel[{n[s],d[s]},s]
指定传递函数模型的分子 n[s] 和分母 d[s].
TransferFunctionModel[{z,p,g},s]
指定传递函数模型的零点 z、极点 p 和增益 g.
给出系统模型 sys 的传递函数模型.


TransferFunctionModel
TransferFunctionModel[g[s],s]
表示具有复数变量 s 的传递函数矩阵 g[s] 的模型.
TransferFunctionModel[{n[s],d[s]},s]
指定传递函数模型的分子 n[s] 和分母 d[s].
TransferFunctionModel[{z,p,g},s]
指定传递函数模型的零点 z、极点 p 和增益 g.
给出系统模型 sys 的传递函数模型.
更多信息和选项


- TransferFunctionModel 通常用于信号滤波器和控制器的设计.
- 可用 TransferFunctionModel[g[s],s] 指定由
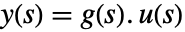 模拟的连续时间系统,其中
模拟的连续时间系统,其中 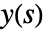 是输出的拉普拉斯变换,
是输出的拉普拉斯变换, 是输入的拉普拉斯变换,
是输入的拉普拉斯变换,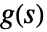 是传递矩阵.
是传递矩阵. - 可用 TransferFunctionModel[g[z],z,SamplingPeriodτ] 指定由
 模拟的离散时间系统,其中
模拟的离散时间系统,其中  是输出的 Z 变换,
是输出的 Z 变换, 是输入的 Z 变换,
是输入的 Z 变换, 是传递矩阵.
是传递矩阵. - 时间延迟可以通过使用 SystemsModelDelay 包含在任意传递函数模型中.
- 在 TransferFunctionModel[sys] 中,可以转换下列系统:
-
AffineStateSpaceModel 近似泰勒转换 NonlinearStateSpaceModel 近似泰勒转换 StateSpaceModel 精确转换 - TransferFunctionModel[…]["prop"] 给出属性 "prop" 的值.
- TransferFunctionModel[…]["Properties"] 给出可用属性的列表.
- 可以选择以下选项:
-
Appearance Automatic 模型的外观 Method Automatic 获得状态-空间模型的传递函数的方法 SamplingPeriod Automatic 系统的采样周期 SystemsModelLabels Automatic 输入和输出变量的标签 ExternalTypeSignature Automatic 嵌入代码的变量类型 - 选项 Appearance 可取以下值:Automatic、"Detailed"、"Structured"、"Elided" 和 "Iconized".
- Method 选项的设置包括 "DeterminantExpansion"、"ResolventIdentities"、"Inverse" 和 "Generic". 当设置 Method->Automatic 时,传递函数模型使用行列式扩展进行计算.
范例
打开所有单元 关闭所有单元范围 (19)
泰勒线性化 AffineStateSpaceModel 并得到其传递函数表达:
AffineStateSpaceModel 有非零平衡常数的线性化:
泰勒线性化 NonlinearStateSpaceModel:
选项 (5)
应用 (18)


属性和关系 (6)
TransferFunctionModel 表现为一个参数的纯函数:
使用 TransferFunctionFactor 获取因子形式:
使用 TransferFunctionCancel 相消共零极点:
Find the element zeros and poles of a transfer-function matrix:
可能存在的问题 (3)
在 TransferFunctionModel[m,var] 中,极点-零点对可能在处理前取消:
使用 Unevaluated 阻止相消:
或者使用 TransferFunctionModel[{num,den},var]:
或者 TransferFunctionModel[{z,p,g},var]:
TransferFunctionModel[m,var] 可能导致更高阶的系统:
或在传给 TransferFunctionModel 前简化 m:
文本
Wolfram Research (2010),TransferFunctionModel,Wolfram 语言函数,https://reference.wolfram.com/language/ref/TransferFunctionModel.html (更新于 2014 年).
CMS
Wolfram 语言. 2010. "TransferFunctionModel." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/TransferFunctionModel.html.
APA
Wolfram 语言. (2010). TransferFunctionModel. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TransferFunctionModel.html 年
BibTeX
@misc{reference.wolfram_2025_transferfunctionmodel, author="Wolfram Research", title="{TransferFunctionModel}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/TransferFunctionModel.html}", note=[Accessed: 19-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_transferfunctionmodel, organization={Wolfram Research}, title={TransferFunctionModel}, year={2014}, url={https://reference.wolfram.com/language/ref/TransferFunctionModel.html}, note=[Accessed: 19-February-2026]}