TreeGame
詳細とオプション







- TreeGameは,展開型ゲーム,逐次手番ゲーム,ゲーム木としても知られている.
- 木ゲームは,プレーヤーが有限個の行動を起すことができる行動ノードとゲームの終了と各プレーヤーの利得を表す終端ノードがある木として説明される.有限数のプレーヤーが交代で有限のゲーム木を生み出す可能性がある.
- TreeGameは,通常,2人以上のプレーヤーが交互に行動する決定問題をモデル化するために使われる.例としてトランプやボードゲームが挙げられるが,市場参入,労働交渉,寡占(市場)行動等もこれに含まれる.
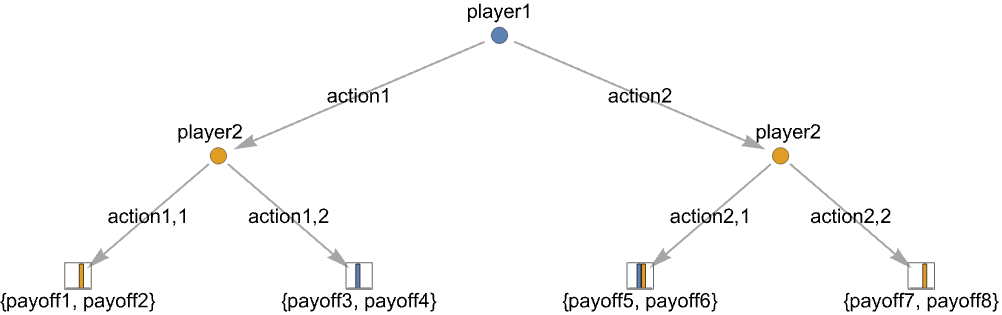
- 次は,可能な行動 actionjである.
-
{playerj,action1,…,actionm} playerjに m 個の可能な行動 actionjがある行動ノード {payoff1,…,payoffn} n 人のプレーヤーの利得が payoffkである終端ノード - 次は,行動ラベルと行動確率を含む行動ノードの追加的な情報である.
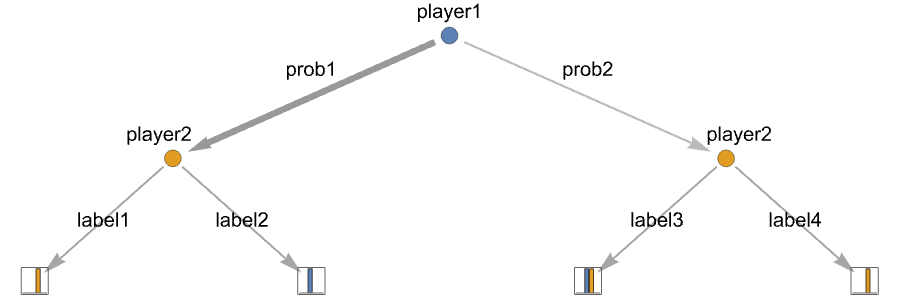
-
{playerj,…,actionilabeli,…} actioniに labeliを使う {playerj,…,actioniprobi,…} 確率 probiの actioniを選ぶ {playerj,…,actioni{labeli,probi},…} ラベルと確率の両方を指定する - 行動ノードで確率的行動を使うときは,すべての行動にその行動ノードの確率がなければならない.
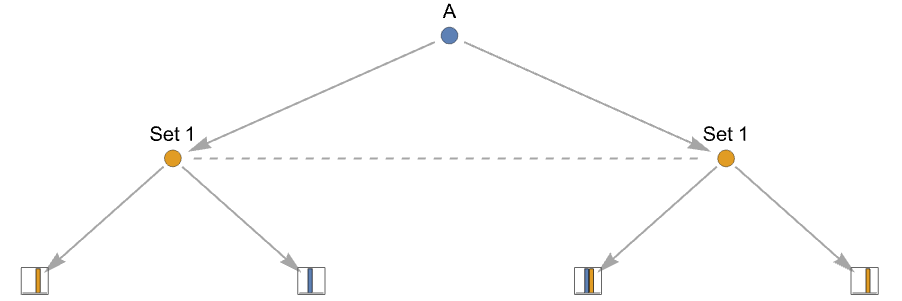
- プレーヤーがどのノードにいるのかについて不完全な情報しかない場合にプレーヤーをモデル化する際は,同じ集合のすべての行動ノードにラベルが付けられた情報集合という概念を使う.
-
{playerjilabelk,action1,…,actionm} 行動ノードに ilabelkを使う - 使用可能な情報集合はゲームの木の同じレベルになければならない.
- 不完全な情報の典型的な例として,他のプレーヤーの手札が分からないので自分がどのノードにいるのか分からないカードゲームが挙げられる.
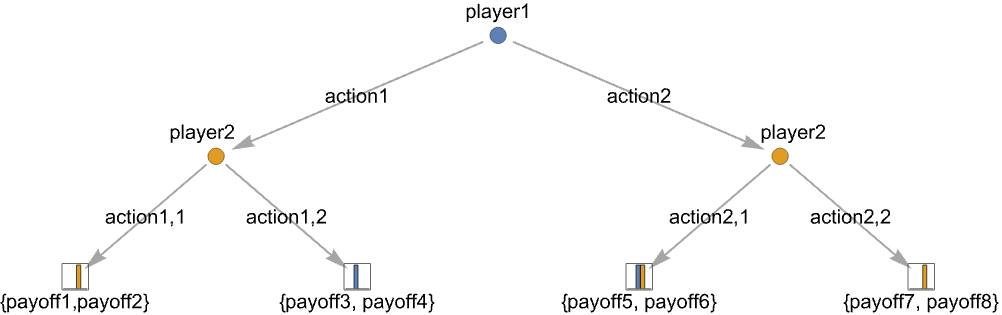
- 別のTree表記を使う.行動木には2つの形があるかもしれない.
-
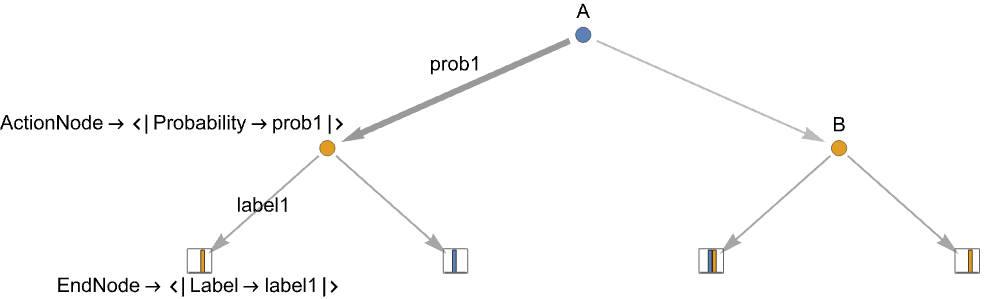
Tree[<|"Player"playerj|>,{actiont1,…,actiontk}] playerjに m 通りの可能な行動 actionjがある行動ノード Tree[<|"Payoffs"{payoff1,…,payoffn}|>,{}] n 人のプレーヤーの利得が payoffkである終端ノード - 行動ノードと終端ノードについての追加情報には,入ってくる辺を参照する行動ラベルと行動確率が含まれる.
-
"Label"label - 親の行動辺に label を使う
"Probability"prob 親の辺に確率 prob を指定 - 行動ノードで確率的行動を使うときは,すべての行動にその行動ノードの確率がなければならない.
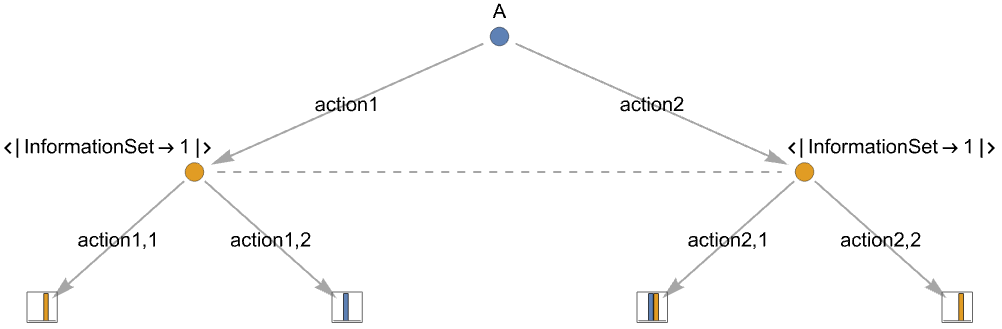
- 不完全な情報は行動ノードで示すことができる.
-
"InformationSet"ilab 行動の木 actiontiの情報集合を指定する - 異なるプレーヤーが同じ情報集合を使った場合,それらは異なる情報集合として扱われる.
- 同じプレーヤーが同じ情報内に行動数が異なるノードを持っている場合,それらは異なる情報集合として扱われる.
- TreeGame g について,次の特性"prop"を g["prop"]として追加することができる.
-
"Graph" ゲームのGraph表現 "InformationSets" 情報集合と含まれているノードの辞書 "MatrixGame" 木ゲームを行列ゲームに変換する "PayoffArray" ゲーム中のすべての利得値のベクトル "Players" プレーヤーのリスト "Plot" ゲームを木プロットとして表現する.TreeGamePlotを見よ "Rules" ゲームのRule表現 "Summary" ゲームの基本データ "Tree" ゲームのTree表現 "Validity" 木ゲームの検証 - TreeGameはTreeGamePlot,FindTreeGameStrategies,VerifyTreeGameStrategy,TreeGamePayoff等の関数で使うことができる.
例題
すべて開く すべて閉じる例 (5)
スコープ (7)
基本的な用法 (4)
特性 (1)
TreeGameオブジェクトは,ゲームについての情報を与える特性を含んでいる:
"Properties"特性は使用可能な特性のリストを与える:
"Object"特性は,ゲームのオブジェクトタイプを与える:
"Summary"特性は,ゲームについての情報の簡単な要約を与える:
"NumberOfPlayers"特性は,ゲームのプレーヤー数を与える:
"NumberOfActions"特性は,ゲームの行動数を与える:
"MinMaxPayoffs"特性は,各プレーヤーの最低利得と最高利得のリストを与える:
"Tree"特性は,ゲームのTree表現を与える:
"Plot"特性は,木ゲームをデフォルトのTreeGamePlotと同じ方法でプロットする:
"MatrixGame"特性は,任意のTreeGameをMatrixGameに変換する:
オプション (2)
アプリケーション (11)
歴史ゲーム (6)
3つのカーテンの一つの後ろに賞品が隠されている.司会者のモンティ・ホール(Monty Hall)が解答者に賞品はどこに隠されているかを尋ねる.司会者は,解答者が推理した後で賞品が隠されているのではないカーテンを一つ開け,推理されたものともう一つのカーテンを閉じたままにして退場する.解答者には,最初の推理通りにするか,もう一つのカーテンを選ぶかの選択肢が与えられる.
エスカレーションゲームは次のように定義される.2国が対立状態にある.片方の国には開始するかしないかの選択肢を持ち,もう片方の国は黙従するかエスカレートするかの選択肢を持つ.第3のプレーヤーである「自然」が利得のランダムさを説明するためにしばしば使われる.このゲームは冷戦時の原子力の脅威に関連して核ゲームとも呼ばれる.
革命ゲームは次のように定義される.植民地には現状に抵抗するかこれを認めるかの選択肢がある.支配国は独立を認めるか抵抗を鎮圧するかできる.植民地が現状を認めた場合,支配国は課税することもしないこともできる.このゲームは,通常,抵抗が鎮圧された場合の利得が不明の状態で研究される.
海軍配置ゲームはビスマルクの戦いゲームを敗走する師団と追撃する師団に拡張したものである.
ビール・キッシュゲームは次のように定義されるシグナリングゲームである.プレーヤーBがプレーヤーAと決闘しようかどうか考えている. BはAが弱虫か荒くれ者かは知らない.BはAが弱虫なら決闘したい.Aは決闘を避けたいと思っている.Bは決断を下す前にAが朝食にビールを飲んだかあるいはキッシュを食べたかを観察する.どちらのプレーヤーも弱虫はキッシュを好み荒くれ者はビールを好むことを知っている.第3のプレーヤーである「自然」が利得のランダムさを説明するためにしばしば使われる.さらに,プレーヤーAはしばしばシグナルの「送り手」,プレーヤーBは「受け手」と呼ばれる.
ボードゲーム (2)
経済ゲーム (2)
関連するガイド
-
▪
- ゲーム理論
テキスト
Wolfram Research (2025), TreeGame, Wolfram言語関数, https://reference.wolfram.com/language/ref/TreeGame.html.
CMS
Wolfram Language. 2025. "TreeGame." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TreeGame.html.
APA
Wolfram Language. (2025). TreeGame. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TreeGame.html
BibTeX
@misc{reference.wolfram_2025_treegame, author="Wolfram Research", title="{TreeGame}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/TreeGame.html}", note=[Accessed: 28-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_treegame, organization={Wolfram Research}, title={TreeGame}, year={2025}, url={https://reference.wolfram.com/language/ref/TreeGame.html}, note=[Accessed: 28-February-2026]}

