TreeGame
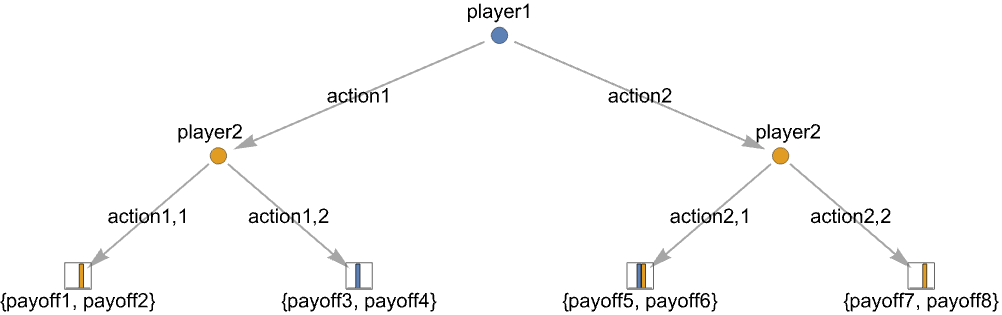
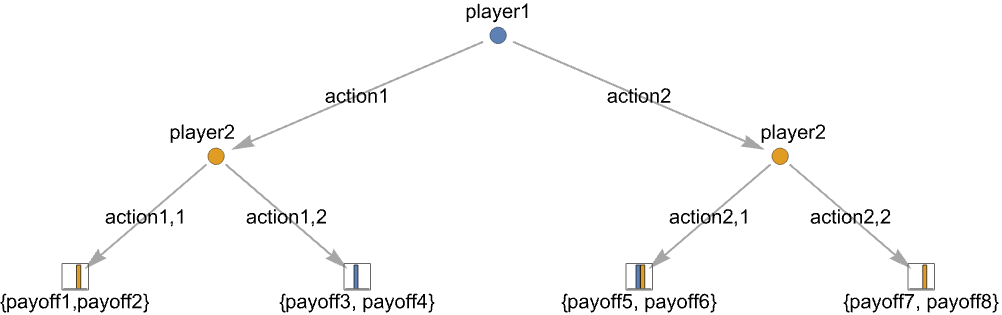
TreeGame[{player1,action1,…,actionk}]
为 player1 指定一个动作节点,其可能的动作为 actionj.
更多信息和选项




- TreeGame 又称为扩展形式博弈、顺序移动博弈或博弈树.
- 树状博弈被描述为一棵树,其中有动作节点和终端节点,在动作节点上玩家可以采取有限数量的行动,而在终端节点上,当博弈结束时每个玩家都会获得收益. 可以有有限数量的多个玩家轮流行动,得到一个有限的博弈树.
- TreeGame 通常用于模拟两个或多个玩家按顺序行动的决策问题. 例子包括纸牌和棋盘游戏,也包括经济或商业博弈,如市场进入、劳资谈判或寡头市场行动等.
- 可能的动作 actionj 包括:
-
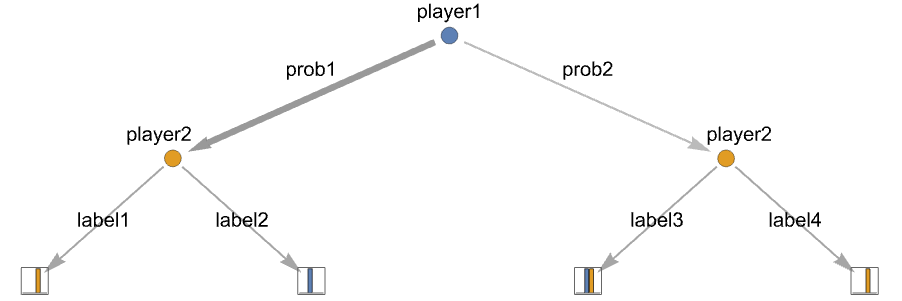
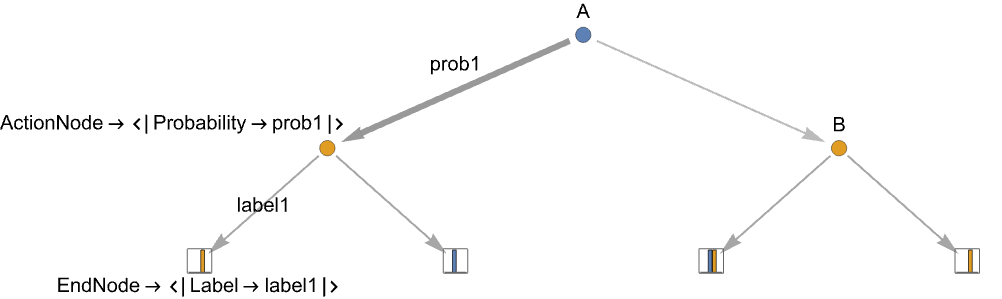
{playerj,action1,…,actionm} 动作节点,其中 playerj 有 m 个可能的动作 actionj {payoff1,…,payoffn} 终端节点,带有 n 个玩家的收益 payoffk - 动作节点的附加信息包括动作标签和动作概率:
-
{playerj,…,actionilabeli,…} 使用 labeli 表示 actioni {playerj,…,actioniprobi,…} 选择 actioni,概率为 probi {playerj,…,actioni{labeli,probi},…} 指定标签和概率 - 当在动作节点使用概率动作时,所有动作都需要具有该动作节点的概率.
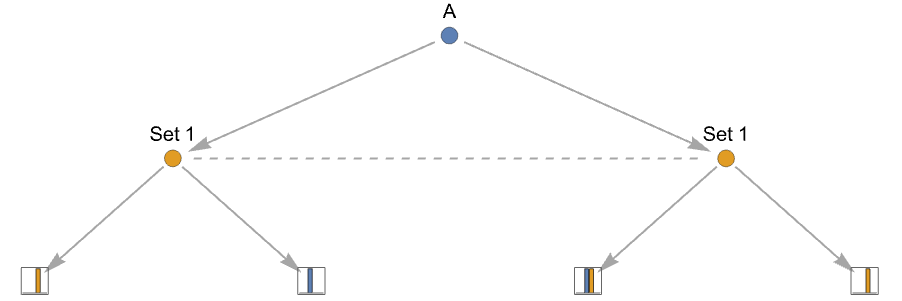
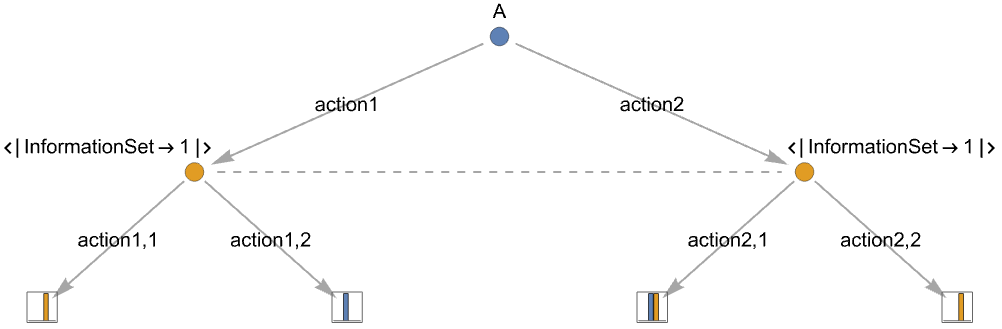
- 为了对玩家所处的节点信息不完全的情况进行建模,这里使用了信息集的概念,它是附加到同一集合中所有动作节点的标签:
-
{playerjilabelk,action1,…,actionm} 使用 ilabelk 作为动作节点 - 可能的信息集需要在博弈树中处于同一级别.
- 不完全信息的一个典型例子是纸牌游戏,你不知道所有玩家的牌,因此不知道自己位于哪个节点.
- 使用替代 Tree 符号,动作树可能有两种形式:
-
Tree[<"Player"playerj>,{actiont1,…,actiontk}] 动作节点,其中 playerj 有 m 个可能的动作 actionj Tree[<"Payoffs"{payoff1,…,payoffn}>,{}] 终端节点,带有 n 个玩家的收益 payoffk - 动作节点和终端节点的附加信息包括引用传入边的动作标签和动作概率:
-
"Label"label 使用 label 作为父动作边 "Probability"prob 指定父边的概率 prob - 当在动作节点使用概率动作时,所有动作都需要具有该动作节点的概率.
- 不完善的信息可以在动作节点中指出:
-
"InformationSet"ilab 指定动作树的信息集 actionti - 如果不同的玩家使用相同的信息集,则将被视为不同的信息集.
- 如果同一个玩家有属于同一个信息集的节点,但是动作数量不同,则会被视为不同的信息集.
- 对于 TreeGame g,以下属性 "prop" 可以通过 g["prop"] 访问:
-
"Graph" 博弈的 Graph 表示 "InformationSets" 包含的信息集和节点的字典 "MatrixGame" 将树博弈转换为矩阵博弈 "PayoffArray" 博弈中所有收益值的向量 "Players" 玩家列表 "Plot" 将博弈表示为树状图;参见 TreeGamePlot "Rules" 博弈的 Rule 表示 "Summary" 博弈的基本数据 "Tree" 博弈的 Tree 表示 "Validity" 树博弈的验证 - TreeGame 可用于 TreeGamePlot、FindTreeGameStrategies、VerifyTreeGameStrategy 和 TreeGamePayoff 等函数.
范例
打开所有单元关闭所有单元基本范例 (5)
范围 (7)
基本用法 (4)
属性 (1)
TreeGame 对象包含提供有关博弈信息的属性:
"NumberOfPlayers" 属性给出博弈中玩家的数量:
"NumberOfActions" 属性给出了博弈中的动作数量:
"MinMaxPayoffs" 给出每个玩家的最小和最大收益列表:
"Tree" 属性给出了博弈的 Tree 表示:
"Plot" 属性以与默认 TreeGamePlot 相同的方式绘制树博弈:
"MatrixGame" 属性将任何 TreeGame 转换为 MatrixGame:
应用 (11)
历史游戏 (6)
奖品隐藏在三扇门中的一扇后面,游戏节目主持人蒙蒂·霍尔会要求您猜出奖品在哪里. 猜完之后,蒙蒂会打开一扇没有隐藏奖品的门,只留下您最初选择的门和另一扇门. 您可以选择保留您最初的选择,也可以切换到另一扇关闭的门.
升级游戏(Escalation game)的定义如下. 两个国家发生冲突。一个国家可以选择主动发起或不主动,另一个国家可以选择默许或升级. 请注意,第三个玩家,“自然”,通常用于描绘收益的随机性. 该游戏也称为核游戏(Nuclear game),指的是冷战期间的原子威胁.
革命游戏(Revolution game)的定义如下. 殖民地可以选择叛乱或接受现状. 国家可以选择给予独立或镇压叛乱. 如果殖民地接受现状,国家可以选择对殖民地征税或不征税. 这种博弈通常在镇压叛乱的收益未知的情况下进行研究.
海军部署游戏(Naval Deployment game)是俾斯麦战役游戏的延伸,其中有一支军队逃跑,另一支军队追击.
啤酒-乳蛋饼游戏(Beer-Quiche game)是一种信号游戏,定义如下. 玩家 B 正在考虑是否与玩家 A 决斗. B 不知道 A 是懦夫还是暴徒. 如果 A 是懦夫,B 更喜欢决斗. 玩家 A 想避免决斗. 首先,B 观察 A 是选择喝啤酒还是吃乳蛋饼当早餐. 两位玩家都知道懦夫更喜欢吃乳蛋饼,而暴徒更喜欢喝啤酒. 请注意,第三个玩家“自然”通常用于描绘 A 类型的随机性. 此外,玩家 A 通常被称为信号的“发送者”,而玩家 B 是“接收者”.
桌游 (2)
经济学博弈 (2)
文本
Wolfram Research (2025),TreeGame,Wolfram 语言函数,https://reference.wolfram.com/language/ref/TreeGame.html.
CMS
Wolfram 语言. 2025. "TreeGame." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/TreeGame.html.
APA
Wolfram 语言. (2025). TreeGame. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TreeGame.html 年