TuttePolynomial
TuttePolynomial[g,{x,y}]
グラフ g のTutte多項式を与える.
TuttePolynomial[{vw,…},…]
規則 vw を使ってグラフ g を指定する.
詳細
- TuttePolynomialは,重クロム多項式あるいはTutte–Whitney多項式としても知られている.
- TuttePolynomial[g]は,g のTutte多項式の純関数表現を与える.
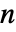 頂点と
頂点と 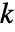 連結成分を持つ無向グラフ
連結成分を持つ無向グラフ 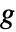 については,Tutte多項式は,
については,Tutte多項式は,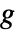 の辺の全部分集合
の辺の全部分集合 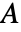 上の
上の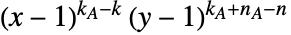 の総和として定義される.
の総和として定義される.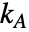 は
は 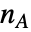 個の頂点を持つ
個の頂点を持つ 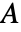 で生成されたグラフの連結成分の数である.
で生成されたグラフの連結成分の数である.
例題
すべて開くすべて閉じるスコープ (6)
アプリケーション (6)
特性と関係 (4)
TuttePolynomial[g,{1,1}]はグラフ中の全域木の数を数える:
TuttePolynomial[g,{2,2}]は2EdgeCount[g]と同等である:
Wolfram Research (2014), TuttePolynomial, Wolfram言語関数, https://reference.wolfram.com/language/ref/TuttePolynomial.html (2015年に更新).
テキスト
Wolfram Research (2014), TuttePolynomial, Wolfram言語関数, https://reference.wolfram.com/language/ref/TuttePolynomial.html (2015年に更新).
CMS
Wolfram Language. 2014. "TuttePolynomial." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/TuttePolynomial.html.
APA
Wolfram Language. (2014). TuttePolynomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TuttePolynomial.html