TuttePolynomial

TuttePolynomial[g,{x,y}]

gives the Tutte polynomial of the graph g.

TuttePolynomial[{vw,…},…]

uses rules vw to specify the graph g.

Details

  • TuttePolynomial is also known as dichromate polynomial or Tutte–Whitney polynomial.
  • TuttePolynomial[g] gives a pure function representation of the Tutte polynomial of g.
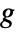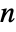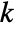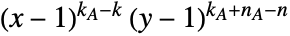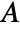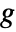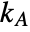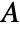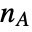  • For an undirected graph with vertices and connected components, the Tutte polynomial is defined as the sum of over all subsets of edges of . is the number of connected components of the graph generated by with vertices.

Examples

open allclose all

Basic Examples  (1)

The Tutte polynomial of a cycle graph:

Plot the contours of the polynomial:

Scope  (6)

TuttePolynomial works with undirected graphs:

Directed graphs:

Multigraphs:

Mixed graphs:

Use rules to specify the graph:

Evaluate at specific values:

Applications  (6)

Find the number of spanning trees of a complete graph:

Cycle graphs:

Wheel graphs:

Find the number of forests of a cycle graph:

Find the number of spanning subgraphs of a cycle graph:

Find the number of acyclic orientations of a cycle graph:

Find the number of strongly connected orientations of a cycle graph:

Compute graph invariant polynomials:

Chromatic polynomials:

Flow polynomials:

Reliability polynomials:

Properties & Relations  (4)

Isomorphic graphs have the same Tutte polynomial:

The Tutte polynomial of a tree with edges is :

TuttePolynomial[g,{1,1}] counts the number of spanning trees in the graph:

TuttePolynomial[g,{2,2}] is equal to 2EdgeCount[g]:

Wolfram Research (2014), TuttePolynomial, Wolfram Language function, https://reference.wolfram.com/language/ref/TuttePolynomial.html (updated 2015).

Text

Wolfram Research (2014), TuttePolynomial, Wolfram Language function, https://reference.wolfram.com/language/ref/TuttePolynomial.html (updated 2015).

CMS

Wolfram Language. 2014. "TuttePolynomial." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/TuttePolynomial.html.

APA

Wolfram Language. (2014). TuttePolynomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TuttePolynomial.html

BibTeX

@misc{reference.wolfram_2024_tuttepolynomial, author="Wolfram Research", title="{TuttePolynomial}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/TuttePolynomial.html}", note=[Accessed: 15-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_tuttepolynomial, organization={Wolfram Research}, title={TuttePolynomial}, year={2015}, url={https://reference.wolfram.com/language/ref/TuttePolynomial.html}, note=[Accessed: 15-November-2024 ]}