TuttePolynomial
TuttePolynomial[g,{x,y}]
给出图 g 的塔特多项式.
TuttePolynomial[{vw,…},…]
用规则 vw 指定图 g.
更多信息
- TuttePolynomial 也称为 dichromate 多项式或者 Tutte–Whitney 多项式.
- TuttePolynomial[g] 给出 g 的塔特多项式的纯函数表示法.
- 对于具有
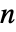 个顶点和
个顶点和 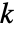 个连通分量的无向图
个连通分量的无向图 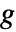 ,塔特多项式定义为
,塔特多项式定义为 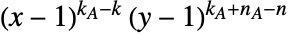 的和,定义为
的和,定义为 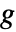 的边组成的所有子集
的边组成的所有子集 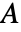 .
. 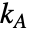 是由具有
是由具有 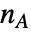 个顶点的
个顶点的 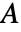 生成的图的连通分量的数目.
生成的图的连通分量的数目.
范例
打开所有单元关闭所有单元范围 (6)
应用 (6)
属性和关系 (4)
TuttePolynomial[g,{1,1}] 计算图中生成树的数目:
TuttePolynomial[g,{2,2}] 等于 2EdgeCount[g]:
Wolfram Research (2014),TuttePolynomial,Wolfram 语言函数,https://reference.wolfram.com/language/ref/TuttePolynomial.html (更新于 2015 年).
文本
Wolfram Research (2014),TuttePolynomial,Wolfram 语言函数,https://reference.wolfram.com/language/ref/TuttePolynomial.html (更新于 2015 年).
CMS
Wolfram 语言. 2014. "TuttePolynomial." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/TuttePolynomial.html.
APA
Wolfram 语言. (2014). TuttePolynomial. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TuttePolynomial.html 年