VoronoiMesh
VoronoiMesh[{p1,…,pn}]
点 p1,p2,…から,ボロノイ(Voronoi)メッシュを表すMeshRegionを与える.
VoronoiMesh[{p1,…,pn},{{xmin,xmax},…}]
メッシュを範囲![]() に切り取る.
に切り取る.
詳細とオプション

- VoronoiMeshは,ボロノイ図,あるいはディリクレ(Dirichlet)分割としても知られている.
- ボロノイメッシュは,それぞれが点 piと関連し
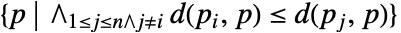 で定義される n 個の凸状セルからなっている.式は,j≠i である任意の他の点 pjよりも piに近い点の領域を表している.
で定義される n 個の凸状セルからなっている.式は,j≠i である任意の他の点 pjよりも piに近い点の領域を表している. - 外側の点と関連しているセルは有界ではないが,有界範囲のみが返される.明示的な範囲{{xmin,xmax},…}が与えられない場合,範囲は自動的に計算される.
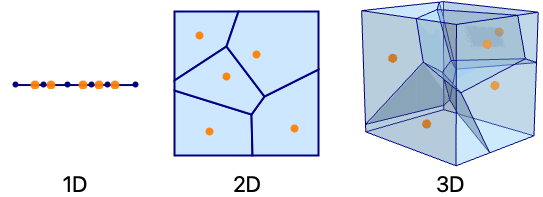
- セルは,1Dにおいては区間,2Dにおいては凸多角形,3Dにおいては凸多面体である.
- VoronoiMeshはMeshRegionと同じオプションを取る.
例題
すべて開くすべて閉じるスコープ (2)
オプション (11)
MeshCellHighlight (2)
MeshCellHighlightを使うとVoronoiMeshの各部分のハイライトを指定することができる:
MeshCellLabel (2)
MeshCellMarker (1)
MeshCellMarkerを使ってVoronoiMeshの各部分に値を割り当てることができる:
MeshCellLabelを使ってマーカーを示す:
MeshCellShapeFunction (2)
MeshCellShapeFunctionを使ってVoronoiMeshの各部分についての関数を指定することができる:
MeshCellStyle (2)
アプリケーション (8)
基本的な応用 (2)
地理 (1)
イタリア内の最も近くにある大都市を示すインタラクティブな地図を作る.イタリアの大都市の名前と座標データを得ることから始める:
領域セルにラベルを付けるためのNearest関数:
画像処理 (1)
先行するボロノイセルの平均の頂点位置にVoronoiMeshを再帰的に適用し,より一様なメッシュを作成する:
その他 (3)
ランダムな点のサンプルの集合上で,関数の区分的に一定な補間を可視化する:
ListContourPlotを使っても同じようなプロットを得ることができる:
ボロノイエッジに沿って障害点のランダム集合を通る点ロボットの経路を考える:
ボロノイエッジから,辺の長さを辺の重みとして無向Graphを作成する:
Nearest関数を使って,始点および終点から最も近いボロノイ頂点を求める:
特性と関係 (6)
VoronoiMeshの出力は,常に全次元のMeshRegionである:
もとのデータの各点が,ボロノイメッシュの厳密に1つのセルに含まれている:
VoronoiMeshはDelaunayMeshの双対である:
各ボロノイセルは,もとになっている点集合の1点を含んでいる:
白い背景上の黒い点についてのDistanceTransformはVoronoiMeshに似ている:
2Dボロノイ図はGraphics3Dでg Coneプリミティブを使って描画できる:
テキスト
Wolfram Research (2014), VoronoiMesh, Wolfram言語関数, https://reference.wolfram.com/language/ref/VoronoiMesh.html (2022年に更新).
CMS
Wolfram Language. 2014. "VoronoiMesh." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/VoronoiMesh.html.
APA
Wolfram Language. (2014). VoronoiMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VoronoiMesh.html