VoronoiMesh

VoronoiMesh[{p1,…,pn}]

给出一个 MeshRegion，它代表由点 p1、p2、… 生成的沃罗诺伊网格.

VoronoiMesh[{p1,…,pn},{{xmin,xmax},…}]

将网格在 的界内进行剪切.

更多信息和选项

  • VoronoiMesh 又被称为沃罗诺伊图和狄利克雷镶嵌.
  • 沃罗诺伊网格由 n 个凸原胞组成，每个原胞都与一个点 pi 相关联并由 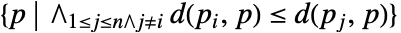定义，即指包含离点 pi 比其他任何点 pj 更近的点集的区域（j≠i）.
  • 与外面点相关联的原胞是无界的，但只返回一个有界的范围. 如果没有给出明确的的范围 {{xmin,xmax},…}，将会自动计算一个范围返回.
  • 单元格将是一维空间中的区间、二维空间中的凸多边形和三维空间中的凸多面体.
  • VoronoiMesh 具有与 MeshRegion 相同的选项.

范例

打开所有单元关闭所有单元

基本范例  (2)

从一组点生成一个一维沃罗诺伊网格：

每个点对应一个沃罗诺伊原胞，在一维的情况下就是一个区间：

从一组点生成一个二维沃罗诺伊网格：

每一个点对应一个沃罗诺伊原胞：

范围  (2)

从一组生成一个一维沃罗诺伊网格：

基本属性：

沃罗诺伊网格是全维的：

沃罗诺伊网格被它们的剪切值所界定：

从一组点生成一个二维沃罗诺伊网格：

基本属性：

沃罗诺伊网格是全维的：

沃罗诺伊网格被它们的剪切值所界定：

选项  (11)

MeshCellHighlight  (2)

MeshCellHighlight 使您可以指定 VoronoiMesh 的一部分的突出显示：

可以使用单元索引突出显示单个单元：

或者通过单元：

MeshCellLabel  (2)

MeshCellLabel 可用于对 VoronoiMesh 的各部分添加标签:

可以使用单元索引对单个单元添加标签：

或者通过单元本身：

MeshCellMarker  (1)

MeshCellMarker 可用于对 VoronoiMesh 的各部分赋值:

使用 MeshCellLabel 显示记号：

MeshCellShapeFunction  (2)

MeshCellShapeFunction 使得你可以指定 VoronoiMesh 各部分的函数:

可以使用单元索引绘制单个单元：

或者通过单元本身：

MeshCellStyle  (2)

MeshCellStyle 使得你可以指定 VoronoiMesh 各部分的样式:

可以使用单元索引突出显示单个单元：

或者通过单元本身：

PlotTheme  (2)

使用具有网格线和图例的主题：

使用某主题绘制边框：

应用  (8)

基本应用  (2)

创建一个带有拖动点的交互式沃罗诺伊网格. 在沃罗诺伊网格上用 Click 添加或删除拖动点：

配置为简单点的含栅格的沃罗诺伊网格：

成一个圆圈的点集：

Geography  (1)

创建一幅意大利最近大城市的交互式地图. 以获得意大利的大城市的名字和坐标作为开始：

标注区域单元的 Nearest 函数:

由城市的坐标创建一个沃罗诺伊网格：

从沃罗诺伊网格生成一个工具提示地图：

鼠标移至地图，得到最近的大城市的名字：

物理  (1)

给定一个二维点阵基底：

生成点阵：

生成并视觉化沃罗诺伊原胞，也称作布里渊区：

图像处理  (1)

从一幅图像生成多边形马赛克图像：

找到图像的边缘：

从边缘位置生成一个沃罗诺伊网格：

对先前沃罗诺伊原胞的平均顶点位置递归应用 VoronoiMesh，进而生成一个更均匀的网格：

给每个多边形涂上与它平均顶点位置相符的图像颜色：

其他  (3)

从一个随机的沃罗诺伊网格生成一个拼图:

从网格中提取直线：

定义一个把一条线转化成互锁边的函数：

用一条互锁边代替足够长的直线：

结果的视觉呈现：

视觉化函数的连续的分段插值（对一组随机点样本）：

从 , 样本坐标生成的沃罗诺伊网格：

将 值重新调整至 的函数：

样本数据的分段连续轮廓图：

通过 ListContourPlot 也能得到相似的绘图：

为点机器人设计一条路径，通过沿着沃罗诺伊边通过一组随机的点障碍物：

在障碍物周围产生沃罗诺伊边：

从沃罗诺伊边（以其长度为权重）生成一幅无向 Graph：

用 Nearest 函数，找到离起始点和结束点最近的沃罗诺伊顶点:

拖动起始点或结束点探索不同的路径（红色）：

属性和关系  (5)

VoronoiMesh 的输出总是一个全维 MeshRegion:

在沃罗诺伊网格中，原始数据的每个点恰好被包含在一个原胞内：

VoronoiMesh 是 DelaunayMesh 的对偶：

每个沃罗诺伊原胞有一个点是来自最初的点的集合：

pi 的沃罗诺伊原胞由 给出：

给每个原胞生成坐标：

背景为白色的黑色点的 DistanceTransform 将与 VoronoiMesh 相似：

Wolfram Research (2014)，VoronoiMesh，Wolfram 语言函数，https://reference.wolfram.com/language/ref/VoronoiMesh.html （更新于 2022 年）.

文本

Wolfram Research (2014)，VoronoiMesh，Wolfram 语言函数，https://reference.wolfram.com/language/ref/VoronoiMesh.html （更新于 2022 年）.

CMS

Wolfram 语言. 2014. "VoronoiMesh." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2022. https://reference.wolfram.com/language/ref/VoronoiMesh.html.

APA

Wolfram 语言. (2014). VoronoiMesh. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/VoronoiMesh.html 年

BibTeX

@misc{reference.wolfram_2024_voronoimesh, author="Wolfram Research", title="{VoronoiMesh}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/VoronoiMesh.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_voronoimesh, organization={Wolfram Research}, title={VoronoiMesh}, year={2022}, url={https://reference.wolfram.com/language/ref/VoronoiMesh.html}, note=[Accessed: 21-November-2024 ]}