WignerD

WignerD[{j,m1,m2},ψ,θ,ϕ]

给出 Wigner D 函数 .

WignerD[{j,m1,m2},θ,ϕ]

给出 Wigner D 函数 .

WignerD[{j,m1,m2},θ]

给出 Wigner D 函数 .

更多信息

  • Wigner D 函数 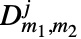给出一个旋转算子的矩阵元素，旋转算子是通过 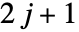维酉表示的旋转群中的欧拉角进行参数化的，其中参数 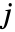、、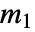 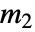是物理的，诸如所有整数或半整数满足 .
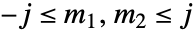  • 对于非物理参数，WignerD 是由解析延拓（analytic continuation）定义的.
  • Wolfram Language 使用相位约定，其中 TemplateBox[{j, {m, _, 1}, {m, _, 2}, psi, theta, phi}, WignerD]=exp(ⅈ m_1 psi+ⅈ m_2phi) TemplateBox[{j, {m, _, 1}, {m, _, 2}, 0, theta, 0}, WignerD].

范例

打开所有单元关闭所有单元

基本范例  (1)

使用整数值物理参数进行运算：

使用半整数物理参数进行运算：

范围  (1)

数值计算物理参数：

推广和延伸  (1)

数值计算非物理参数：

应用  (1)

构建一个自旋 1/2 表示的旋转矩阵：

检查酉性：

根据旋量构建一个三维向量：

旋量基转换成坐标基：

由旋量的酉变换引起的坐标变换：

使用欧拉角直接构建结果旋转矩阵：

属性和关系  (4)

对于消失参数 m1，WignerD 简化为 SphericalHarmonicY：

Wigner D 矩阵的矩阵元素满足一定的对称关系：

WignerD 函数构成 组上的一个正交基：

积分等于 2/(2 j_1+1) (4 pi)^2TemplateBox[{{{j, _, 1}, ,, {j, _, 2}}}, KroneckerDeltaSeq]TemplateBox[{{{m, _, {(, 11, )}}, ,, {m, _, {(, 21, )}}}}, KroneckerDeltaSeq]TemplateBox[{{{m, _, {(, 12, )}}, ,, {m, _, {(, 22, )}}}}, KroneckerDeltaSeq]：

两个 WignerD 函数之积可以利用 ClebschGordan 系数以 WignerD 函数的形式展开：

Wolfram Research (2010)，WignerD，Wolfram 语言函数，https://reference.wolfram.com/language/ref/WignerD.html.

文本

Wolfram Research (2010)，WignerD，Wolfram 语言函数，https://reference.wolfram.com/language/ref/WignerD.html.

CMS

Wolfram 语言. 2010. "WignerD." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/WignerD.html.

APA

Wolfram 语言. (2010). WignerD. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/WignerD.html 年

BibTeX

@misc{reference.wolfram_2024_wignerd, author="Wolfram Research", title="{WignerD}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/WignerD.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_wignerd, organization={Wolfram Research}, title={WignerD}, year={2010}, url={https://reference.wolfram.com/language/ref/WignerD.html}, note=[Accessed: 17-November-2024 ]}