"HashSet" (Data Structure)
"HashSet"
represents a set where the members are general expressions and membership is computed by using a hash function.
Details

- A hash set is useful for efficient insertion and removal as well as membership testing:
-
CreateDataStructure["HashSet"] create a new empty "HashSet" CreateDataStructure["HashSet",elems] create a new "HashSet" containing elems Typed[x,"HashSet"] give x the type "HashSet" - For a data structure of type "HashSet", the following operations can be used:
-
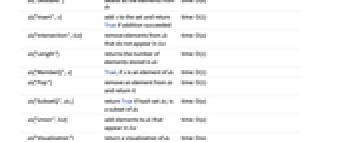
ds["Complement",list] remove elements from ds that appear in list time: O(n) ds["Copy"] return a copy of ds time: O(n) ds["Elements"] return a list of the elements of ds time: O(n) ds["EmptyQ"] True, if ds has no elements time: O(1) ds["Delete",x] delete x from ds, return True if x was actually an element time: O(1) ds["DeleteAll"] delete all the elements from ds time: O(n) ds["Insert",x] add x to the set and return True if addition succeeded time: O(1) ds["Intersection",list] remove elements from ds that do not appear in list time: O(n) ds["Length"] returns the number of elements stored in ds time: O(1) ds["MemberQ",x] True, if x is an element of ds time: O(1) ds["Pop"] remove an element from ds and return it time: O(1) ds["SubsetQ",ds1] return True if hash set ds1 is a subset of ds time: O(n) ds["Union",list] add elements to ds that appear in list time: O(n) ds["Visualization"] return a visualization of ds time: O(n) - The following functions are also supported:
-
dsi===dsj True, if dsi equals dsj FullForm[ds] full form of ds Information[ds] information about ds InputForm[ds] input form of ds Normal[ds] convert ds to a normal expression
Examples
open all close allBasic Examples (2)
A new "HashSet" can be created with CreateDataStructure:
There is one element in the set:
Test if an expression is stored:
If an expression is not stored, False is returned:
Remove an element from the set. If something was actually removed, return True:
Return an expression version of ds:
Scope (2)
Information (1)
A new "HashSet" can be created with CreateDataStructure:
Set Operations (1)
"HashSet" supports some core set operations. A new empty "HashSet" can be created with CreateDataStructure.
The "Union" operation adds elements that were not originally in the data structure:
The "Complement" operation removes elements from the data structure:
The "Intersection" operation leaves common elements in the data structure:
Applications (1)
See Also
Association Dispatch Hash DownValues CreateDataStructure DataStructure
Data Structures: OrderedHashSet HashTable OrderedHashTable DisjointSet SortedMultiset
Related Guides
History
Introduced in 2020 (12.1)