"LinearRegression" (機械学習メソッド)

詳細とサブオプション

  • 線形回帰は数値的特徴 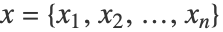を組み合せることで数値出力 y を予測する．条件付き確率 は 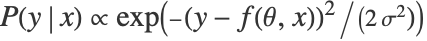に従ってモデル化される．ただし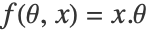， である．
  • パラメータベクトル θ の推定は，損失関数1/2sum_(i=1)^m(y_i-f(theta,x_i))^2+lambda_1sum_(i=1)^nTemplateBox[{{theta, _, i}}, Abs]+(lambda_2)/2 sum_(i=1)^ntheta_i^2を最小にすることで行われる． m は例の数，n は数値的特徴の数である．
  • 次は，使用可能なサブオプションである．
  • "L1Regularization" 0損失関数中の 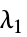の値
    "L2Regularization" Automatic損失関数中の 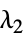の値
    "OptimizationMethod" Automatic使用する最適化メソッド
  • "OptimizationMethod"オプションの可能な設定には次がある．
  • "NormalEquation"線形代数メソッド
    "StochasticGradientDescent"確率勾配メソッド
    "OrthantWiseQuasiNewton"象限ごとの擬似ニュートンメソッド
  • このメソッドについては，Information[PredictorFunction[…],"Function"]は特徴から予測値を計算する簡単な式を与える．

例題

すべて開くすべて閉じる

例  (2)

ラベル付きの例で予測器を訓練する：

Informationを見る：

新たな例を予測する：

二次元データを生成する：

このデータで予測器関数を訓練する：

データを予測された値と比較し，標準偏差を見る：

オプション  (5)

"L1Regularization"  (2)

"L1Regularization"オプションを使って予測器を訓練する：

訓練集合を生成し，可視化する：

"L1Regularization"の値を変えて2つの予測器を訓練する：

L1正規化を大きくすることで1つのパラメータがどのように強制的に0になったかを見るために，予測器関数を見る：

"L2Regularization"  (2)

"L2Regularization"オプションを使って予測器を訓練する：

訓練集合を生成し，可視化する：

"L2Regularization"オプションの値を変えて2つの予測器を訓練する：

L2正規化がパラメータベクトルのノルムをどのように減じたかを見るために，予測器関数を見る：

"OptimizationMethod"  (1)

大きい訓練集合を生成する：

異なる最適化メソッドで予測器を訓練し，訓練時間を比較する：