Audio Synthesis

OscillatorsProcesses and Time Series
Noise GeneratorsAdvanced Synthesis
The Wolfram Language provides extensive support for the creation, analysis, and manipulation of audio data, fully integrated with the Wolfram Language's powerful mathematical and algorithmic capabilities.
The starting point for audio synthesis is the AudioGenerator function.
AudioGenerator[model]
generates one second of audio of a given model
AudioGenerator[model,t]
generates t seconds of audio
Audio generation.
Oscillators
The simplest way to generate a signal is to use one of the native oscillator models supported in AudioGenerator.
Generate a sinusoidal signal:
Generate a sinusoidal signal of a specific frequency:
Different oscillator models have different harmonic contents:
All oscillator models accept time-varying parameters for frequency and phase: the input can be a TimeSeries, another Audio object, or even a pure function.
Use an audio signal to control the frequency:
Use a pure function to control the frequency:
Use a time series to control the frequency:
Noise Generators
In addition to oscillators, AudioGenerator allows for the creation of different kinds of noise signals.
Generate one second of pink noise:
Different types of noise have different spectral contents:
White noise is characterized by a flat spectrum. By default, sample values are picked from a uniform distribution, but it is possible to change that without affecting the spectrum.
White noise with amplitudes sampled from a normal distribution:
Plot the histogram and the periodogram of the signal:
Using {"Color",α} will generate a "colored" noise signal whose spectrum follows a f-α distribution. "Pink", "Brown", and "Blue" are instances of colored noise, where the α has values of 1, 2, and .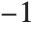
Change the "color" of the noise:
Processes and Time Series
AudioGenerator can be used to generate a signal by sampling a random process.
Generate an audio signal from a discrete-time or continuous-time process:
AudioGenerator can also be used to create an Audio object from a TimeSeries.
Create an audio signal starting from a TimeSeries:
Advanced Synthesis

Subtractive Synthesis

By processing an audio object with one or more frequency-selective filters, it is possible to manipulate its harmonic content and therefore change its timbre. This technique is effective if the starting audio object is harmonically rich.
Filter a sawtooth wave:
Use two different filters on a square waveform:

Additive Synthesis

In contrast to subtractive synthesis where harmonics are attenuated using filters, additive synthesis is based on the addition of harmonics. The effect is obtained with linear combination of sine waves at different frequencies, where the user has control over the coefficients of the linear combination.
Control the amplitudes of the first 8 harmonics of a 200 Hz fundamental:

Amplitude Modulation

Amplitude modulation (AM) is a common technique to create signals with complex harmonic content.
In AM, two signals are used, called carrier and modulator. The result is computed using carrier(1+μmodulator), where the scaling constant μ is called modulation index.
If the modulator is a sinusoid, for each component of the carrier at a frequency f, a pair of sidebands is created at frequencies f±m, whose amplitude is controlled by the modulation index.
Amplitude modulation of a triangle wave:
Plot the periodogram of the signal:

Frequency Modulation

Another popular technique, discovered in the early 1970s, uses frequency modulation (FM).
In the case of FM, the frequency of the carrier signal is controlled by the modulator and the modulation index. As the modulation index increases, sidebands occur above and below the carrier frequency at intervals of the modulating frequency.
Basic frequency modulation:
Plot the periodogram of the signal:
The number and intensity of these additional sidebands are related to the modulation index.
Use a higher modulation amount to increase sideband amplitude:
The position of the sidebands is determined by the ratio between the carrier and modulator frequencies. Changing this ratio, it is possible to obtain both harmonic (typical of pitched instruments) and inharmonic (typical of percussive instruments) spectra.
Create harmonic and inharmonic signals:
If the modulation index becomes a time-varying argument, it becomes easy to generate signals whose harmonic content evolves with time.
Increase the bandwidth of the signal by incrementing the modulation index:
Plot the spectrogram of the result:
The modulating frequency can be a time-varying parameter as well.
Change the position of the sidebands by varying the modulating frequency:
Plot the spectrogram of the result: