Audio Basics
Audio Basics
The Wolfram Language provides built-in support for both programmatic and interactive audio processing, fully integrated with the Wolfram Language's powerful mathematical and algorithmic capabilities. You can create and import sound files, manipulate them with built-in functions, apply linear and nonlinear filters, and visualize them in any number of ways.
| Audio[data] | in-core audio with samples given by data |
| Audio[file] | out-of-core audio from a file |
| Audio[url] | out-of-core audio from a url |
| Import[file] | import audio from a file |
| AudioGenerator[model] | generate various oscillators and noises |
The simplest way to create an audio object is to wrap the Audio constructor around a vector of real values ranging from 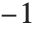 to 1.
to 1.
Another way is to obtain an out-of-core audio object from a file on the local file system or any accessible remote location. Out-of-core audio objects do not store samples in memory.
This creates an out-of-core audio object from the Wolfram Language documentation directory ExampleData and displays the number of bytes used internally by the object:
You can use Import to create an in-core audio object from a file or URL.
This creates an in-core audio object and displays the number of bytes used internally by the object:
This converts sound represented by SampledSoundFunction to audio:
Various oscillators and noises can be created using AudioGenerator.
| AudioLength[audio] | give the number of samples of an audio object |
| Duration[audio] | give the duration of audio in seconds |
| AudioChannels[audio] | give the number of channels present in the data for audio |
| AudioSampleRate[audio] | give the sample rate associated with audio |
| AudioType[audio] | give the type of values used for each sample element in audio |
The array of sample values can be extracted using the function AudioData. By default, the function returns real values, but you can ask for a specific type using the optional "type" argument.
Here is the same fragment extracted from the out-of-core audio as a vector of integers in the range –127 to 128:
In the case of multichannel audio, the raw sample data is represented by a list of channel values (2D array).
This creates an out-of-core multichannel audio object and extracts a fragment of that audio object as a list of channel values:
A multichannel audio object can be split into a list of single-channel audio objects and conversely, a multichannel audio object can be created from any number of single-channel audio objects.
| AudioPlot[audio] | plot the waveform of audio |
| Periodogram[audio] |
plot the squared magnitude of the discrete Fourier transform (power spectrum) of
audio
|
| Spectrogram[audio] | plot the spectrogram of audio |
Many useful audio processing tasks require nothing more than simple arithmetic operations between two audio objects or an audio object and a constant. For example, you can change volume by multiplying an audio object by a constant factor or by adding (subtracting) a constant to (from) an audio object. For this purpose, all Wolfram Language operators and functions with attributes NumericFunction or Listable are overloaded to work with audio objects.
| audio1+audio2 | add two audio objects |
| n*audio | multiply a scalar by an audio object |
| Mean[{a1,a2,…}] | compute the mean of a list of audio objects |
A system option called "IndeterminateValue" is used to replace values that can result from arithmetical operation but cannot be stored in an audio object. These include ComplexInfinity and Indeterminate.
This shows how "IndeterminateValue" is used to replace unacceptable values in the result of an arithmetical operation:
Complex numbers in the result of an arithmetical operation are replaced by the real parts of these values:
Consider the audio manipulation operations that change the audio duration by trimming, deleting, or padding. These operations serve a variety of useful purposes. Trimming and deleting allow you to create a new audio object from a selected portion of a larger one, while padding is typically used to extend an audio object at the ends to ensure uniform treatment of the end samples in many audio processing tasks.
| AudioTrim[audio,{t1,t2}] | give an audio object consisting of only samples between t1 and t2 |
| AudioPad[audio,m] | pad audio on both sides with m seconds of zeros |
| AudioDelete[audio,{t1,t2}] | delete from time t1 to time t2 |
| AudioSplit[audio,{t1,t2,…}] | split audio at times ti |
| AudioPartition[audio,dur,offset] | partition audio into overlapping segments |
| AudioIntervals[audio,crit] | return intervals of audio for which criteria crit is satisfied |
Intervals that satisfy various criteria can be computed and used to extract corresponding blocks of an audio object.
This computes the intervals where the maximal value is greater than .1 and the value of the spectral centroid is smaller than 800:
It is frequently necessary to change the sample rate of an audio object by resampling, or to normalize audio samples in some manner. Functions that perform these basic tasks are readily available.
| AudioResample[audio,sr] | give a resampled audio object that has sample rate sr |
| AudioNormalize[audio] | normalize audio so that the maximum absolute value of its samples is 1 |
| AudioAmplify[audio,s] | multiply all samples of the audio by a factor s |
| AudioJoin[list] | concatenate a list of audio objects |
| AudioOverlay[list] | overlay a list of audio objects |
| ConformAudio[list] | conform properties of each audio object from the list |