Graphics and Sound
Graphics and Sound
| Basic Plotting | Plotting Lists of Data |
| Options for Graphics | Parametric Plots |
| Redrawing and Combining Plots | Some Special Plots |
| Three‐Dimensional Surface Plots | Sound |
| Plot[f,{x,xmin,xmax}] | plot f as a function of x from xmin to xmax |
| Plot[{f1,f2,…},{x,xmin,xmax}] | plot several functions together |
You can plot functions that have singularities. The Wolfram Language will try to choose appropriate scales:
The singularities can be omitted from the plot by using the Exclusions option:
You can give a list of functions to plot. A different color will automatically be used for each function:
This finds the numerical solution to a differential equation, as discussed in "Numerical Differential Equations":
When the Wolfram Language plots a graph for you, it has to make many choices. It has to work out what the scales should be, where the function should be sampled, how the axes should be drawn, and so on. Most of the time, the Wolfram Language will probably make pretty good choices. However, if you want to get the very best possible pictures for your particular purposes, you may have to help the Wolfram Language in making some of its choices.
There is a general mechanism for specifying "options" in Wolfram Language functions. Each option has a definite name. As the last arguments to a function like Plot, you can include a sequence of rules of the form name->value, to specify the values for various options. Any option for which you do not give an explicit rule is taken to have its "default" value.
| Plot[f,{x,xmin,xmax},option->value] |
make a plot, specifying a particular value for an option
|
A function like Plot has many options that you can set. Usually you will need to use at most a few of them at a time. If you want to optimize a particular plot, you will probably do best to experiment, trying a sequence of different settings for various options.
Each time you produce a plot, you can specify options for it. "Redrawing and Combining Plots" will also discuss how you can change some of the options, even after you have produced the plot.
option name | default value | |
| AspectRatio | 1/GoldenRatio | |
| Axes | True | whether to include axes |
| AxesLabel | None | labels to be put on the axes; ylabel specifies a label for the |
| AxesOrigin | Automatic | the point at which axes cross |
| BaseStyle | {} | the default style to use for the plot |
| FormatType | TraditionalForm | the default format type to use for text in the plot |
| Frame | False | whether to draw a frame around the plot |
| FrameLabel | None | labels to be put around the frame; give a list in clockwise order starting with the lower |
| FrameTicks | Automatic | what tick marks to draw if there is a frame; None gives no tick marks |
| GridLines | None | what grid lines to include; Automatic includes a grid line for every major tick mark |
| PlotLabel | None | an expression to be printed as a label for the plot |
| PlotRange | Automatic | the range of coordinates to include in the plot; All includes all points |
| Ticks | Automatic | what tick marks to draw if there are axes; None gives no tick marks |
This specifies labels for the  and
and 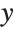 axes. The expressions you give as labels are printed just as they would be if they appeared as TraditionalForm Wolfram Language output. You can give any piece of text by putting it inside a pair of double quotes:
axes. The expressions you give as labels are printed just as they would be if they appeared as TraditionalForm Wolfram Language output. You can give any piece of text by putting it inside a pair of double quotes:
Setting the AspectRatio option changes the whole shape of your plot. AspectRatio gives the ratio of height to width. Its default value is the inverse of the Golden Ratio—supposedly the most pleasing shape for a rectangle:
| Automatic | use internal algorithms |
| None | do not include this |
| All | include everything |
| True | do this |
| False | do not do this |
When the Wolfram Language makes a plot, it tries to set the 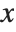 and
and 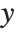 scales to include only the "interesting" parts of the plot. If your function increases very rapidly, or has singularities, the parts where it gets too large will be cut off. By specifying the option PlotRange, you can control exactly what ranges of
scales to include only the "interesting" parts of the plot. If your function increases very rapidly, or has singularities, the parts where it gets too large will be cut off. By specifying the option PlotRange, you can control exactly what ranges of 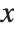 and
and 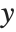 coordinates are included in your plot.
coordinates are included in your plot.
| Automatic |
show at least a large fraction of the points, including the "interesting" region (the default setting)
|
| All | show all points |
| {ymin,ymax} | show a specific range of |
| {xrange,yrange} | show the specified ranges of |
Settings for the option PlotRange.
The setting for the option PlotRange gives explicit 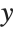 limits for the graph. With the
limits for the graph. With the 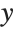 limits specified here, the bottom of the curve is cut off:
limits specified here, the bottom of the curve is cut off:
The Wolfram Language always tries to plot functions as smooth curves. As a result, in places where your function wiggles a lot, the Wolfram Language will use more points. In general, the Wolfram Language tries to adapt its sampling of your function to the form of the function. There is a limit, however, which you can set, to how finely the Wolfram Language will ever sample a function.
The function 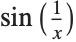 wiggles infinitely often when
wiggles infinitely often when  . the Wolfram Language tries to sample more points in the region where the function wiggles a lot, but it can never sample the infinite number that you would need to reproduce the function exactly. As a result, there are slight glitches in the plot:
. the Wolfram Language tries to sample more points in the region where the function wiggles a lot, but it can never sample the infinite number that you would need to reproduce the function exactly. As a result, there are slight glitches in the plot:
It is important to realize that since the Wolfram Language can only sample your function at a limited number of points, it can always miss features of the function. The Wolfram Language adaptively samples the functions, increasing the number of samples near interesting features, but it is still possible to miss something. By increasing PlotPoints, you can make the Wolfram Language sample your function at a larger number of points. Of course, the larger you set PlotPoints to be, the longer it will take the Wolfram Language to plot any function, even a smooth one.
option name | default value | |
| PlotStyle | Automatic |
a list of lists of graphics primitives to use for each curve (see
"Graphics Directives and Options"
)
|
| ClippingStyle | None | what to draw when curves are clipped |
| Filling | None | filling to insert under each curve |
| FillingStyle | Automatic | style to use for filling |
| PlotPoints | 50 | the initial number of points at which to sample the function |
| MaxRecursion | Automatic | the maximum number of recursive subdivisions allowed |
This uses PlotStyle to specify a dashed curve:
When plotting multiple functions, PlotStyle settings in a list are used sequentially for each function:
When a PlotStyle contains a sublist, the settings are combined:
By default nothing is indicated when the PlotRange is set, so that it cuts off curves:
Setting ClippingStyle to a list defines the style for the parts cut off at the bottom and top:
The filling can be specified to extend to an arbitrary height, such as the bottom of the graphic. Filling colors are automatically blended where they overlap:
The Wolfram Language saves information about every plot you produce, so that you can later redraw it. When you redraw plots, you can change some of the options you use.
| Show[plot,option->value] | redraw a plot with options changed |
| Show[plot1,plot2,…] | combine several plots |
| GraphicsGrid[{{plot1,plot2,…},…}] | draw an array of plots |
| InputForm[plot] | show the underlying textual description of the plot |
By using Show with a sequence of different options, you can look at the same plot in many different ways. You may want to do this, for example, if you are trying to find the best possible setting of options.
You can also use Show to combine plots. All of the options for the resulting graphic will be based upon the options of the first graphic in the Show expression.
All Wolfram Language graphics are expressions and can be manipulated in the same way as any other expression. Doing these kinds of manipulations does not require the use of Show.
This replaces all instances of the symbol Line with the symbol Point in the graphics expression represented by gj0:
Using Show[plot1,plot2,…] you can combine several plots into one. GraphicsGrid allows you to draw several plots in an array.
| GraphicsGrid[{{plot11,plot12,…},…}] | draw a rectangular array of plots |
| GraphicsRow[{plot1,plot2,…}] | draw several plots side by side |
| GraphicsColumn[{plot1,plot2,…}] | draw a column of plots |
| GraphicsGrid[plots,Spacings->{h,v}] | put the specified horizontal and vertical spacing between the plots |
If you redisplay an array of plots using Show, any options you specify will be used for the whole array, rather than for individual plots:
GraphicsGrid by default puts a narrow border around each of the plots in the array it gives. You can change the size of this border by setting the option Spacings->{h,v}. The parameters h and v give the horizontal and vertical spacings to be used. The Spacings option uses the width and height of characters in the default font to scale the h and v parameters by default, but it is generally more useful in graphics to use Scaled coordinates. Scaled scales widths and heights so that a value of 1 represents the width and height of one element of the grid.
This increases the horizontal spacing, but decreases the vertical spacing between the plots in the array:
When you make a plot, the Wolfram Language saves the list of points it used, together with some other information. Using what is saved, you can redraw plots in many different ways with Show. However, you should realize that no matter what options you specify, Show still has the same basic set of points to work with. So, for example, if you set the options so that the Wolfram Language displays a small portion of your original plot magnified, you will probably be able to see the individual sample points that Plot used. Options like PlotPoints can only be set in the original Plot command itself. (the Wolfram Language always plots the actual points it has; it avoids using smoothed or splined curves, which can give misleading results in mathematical graphics.)
This shows a small region of the plot in a magnified form. At this resolution, you can see the individual line segments that were produced by the original Plot command:
| Plot3D[f,{x,xmin,xmax},{y,ymin,ymax}] | |
make a three‐dimensional plot of f as a function of the variables x and y | |
Three-dimensional graphics can be rotated in place by dragging the mouse inside the graphic. Dragging inside the graphic causes the graphic to tumble in a direction that follows the mouse, and dragging around the borders of the graphic causes the graphic to spin in the plane of the screen. Dragging the graphic while holding down the Shift key causes the graphic to pan. Use the Ctrl key to zoom.
There are many options for three‐dimensional plots in the Wolfram System. Some are discussed here; others are described in "The Structure of Graphics and Sound".
The first set of options for three‐dimensional plots is largely analogous to those provided in the two‐dimensional case.
option name | default value | |
| Axes | True | whether to include axes |
| AxesLabel | None | labels to be put on the axes: zlabel specifies a label for the |
| BaseStyle | {} | the default style to use for the plot |
| Boxed | True | whether to draw a three-dimensional box around the surface |
| FaceGrids | None | how to draw grids on faces of the bounding box; All draws a grid on every face |
| LabelStyle | {} | style specification for labels |
| Lighting | Automatic | simulated light sources to use |
| Mesh | Automatic | whether an |
| PlotRange | {Full,Full,Automatic} | the range of |
| SphericalRegion | False | whether to make the circumscribing sphere fit in the final display area |
| ViewAngle | All | angle of the field of view |
| ViewCenter | {1,1,1}/2 | point to display at the center |
| ViewPoint | {1.3,-2.4,2} | the point in space from which to look at the surface |
| ViewVector | Automatic | position and direction of a simulated camera |
| ViewVertical | {0,0,1} | direction to make vertical |
| BoundaryStyle | Automatic | how to draw boundary lines for surfaces |
| ClippingStyle | Automatic | how to draw clipped parts of surfaces |
| ColorFunction | Automatic | how to determine the color of the surfaces |
| Filling | None | filling under each surface |
| FillingStyle | Opacity[.5] | style to use for filling |
| PlotPoints | 25 | the number of points in each direction at which to sample the function; |
| PlotStyle | Automatic | graphics directives for the style of each surface |
This redraws the previous plot with options changed. With this setting for PlotRange, only the part of the surface in the range  is shown:
is shown:
When you make the original plot, you can choose to sample more points. The Wolfram System adaptively samples the plot, adding points for large variations, but occasionally you may still need to specify a greater number of points:
Probably the single most important issue in plotting a three‐dimensional surface is specifying where you want to look at the surface from. The ViewPoint option for Plot3D and Show allows you to specify the point 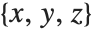 in space from which you view a surface. The details of how the coordinates for this point are defined are discussed in "Coordinate Systems for Three-Dimensional Graphics". When rotating a graphic using the mouse, you are adjusting the ViewPoint value.
in space from which you view a surface. The details of how the coordinates for this point are defined are discussed in "Coordinate Systems for Three-Dimensional Graphics". When rotating a graphic using the mouse, you are adjusting the ViewPoint value.
Here is a surface, viewed from the default view point {1.3,-2.4,2}. This view point is chosen to be "generic", so that visually confusing coincidental alignments between different parts of your object are unlikely:
This redraws the picture, with the view point directly in front. Notice the perspective effect that makes the back of the box look much smaller than the front:
The ViewPoint option also accepts various symbolic values that represent common view points:
| {1.3,-2.4,2} | default view point |
| Front | in front, along the negative |
| Back | in back, along the positive |
| Above | above, along the positive |
| Below | below, along the negative |
| Left | left, along the negative |
| Right | right, along the positive |
Typical choices for the ViewPoint option.
The human visual system is not particularly good at understanding complicated mathematical surfaces. As a result, you need to generate pictures that contain as many clues as possible about the form of the surface.
View points slightly above the surface usually work best. It is generally a good idea to keep the view point close enough to the surface that there is some perspective effect. Having a box explicitly drawn around the surface is helpful in recognizing the orientation of the surface.
This shows the surface without the mesh drawn. It is usually much harder to see the form of the surface if the mesh is not there:
To add an extra element of realism to three‐dimensional graphics, the Wolfram System by default colors three‐dimensional surfaces using a simulated lighting model. In the default case, the Wolfram System assumes that there are four point light sources plus ambient lighting shining on the object. "Lighting and Surface Properties" describes how you can set up other light sources, and how you can specify the reflection properties of an object.
Lighting can also be specified using a string that represents a collection of lighting properties. For example, the option setting Lighting->"Neutral" uses a set of white lights, and so can be faithfully reproduced on a black and white output device such as a printer.
The ColorFunction option by default uses Lighting->"Neutral" so that the surface colors are not distorted by colored lights:
The Wolfram Language can be used to make plots of functions. You give the Wolfram Language a function, and it builds up a curve or surface by evaluating the function at many different points.
Here we describe how you can make plots from lists of data, instead of functions. ("Importing and Exporting Data" discusses how to read data from external files and programs.) The Wolfram Language commands for plotting lists of data are direct analogs of the ones for plotting functions.
| ListPlot[{y1,y2,…}] | plot y1,y2,… at x values 1,2,… |
| ListPlot[{{x1,y1},{x2,y2},…}] | plot points (x1,y1),… |
| ListLinePlot[list] | join the points with lines |
| ListPlot3D[{{z11,z12,…},{z21,z22,…},…}] | |
make a three‐dimensional plot of the array of heights zyx | |
| ListPlot3D[{{x1,y1,z1},{x2,y2,z2},…}] | |
make a three-dimensional plot with heights zi at positions {xi,yi} | |
| ListContourPlot[array] | make a contour plot |
| ListDensityPlot[array] | make a density plot |
When plotting multiple datasets, the Wolfram Language chooses a different color for each dataset automatically:
This gives a rectangular array of values. The array is quite large, so we end the input with a semicolon to stop the result from being printed out:
"Basic Plotting" describes how to plot curves in the Wolfram Language in which you give the 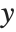 coordinate of each point as a function of the
coordinate of each point as a function of the 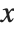 coordinate. You can also use the Wolfram Language to make parametric plots. In a parametric plot, you give both the
coordinate. You can also use the Wolfram Language to make parametric plots. In a parametric plot, you give both the 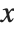 and
and 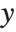 coordinates of each point as a function of a third parameter, say
coordinates of each point as a function of a third parameter, say 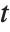 .
.
| ParametricPlot[{fx,fy},{t,tmin,tmax}] | |
make a parametric plot | |
| ParametricPlot[{{fx,fy},{gx,gy},…},{t,tmin,tmax}] | |
plot several parametric curves together | |
Here is the curve made by taking the  coordinate of each point to be Sin[t] and the
coordinate of each point to be Sin[t] and the 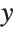 coordinate to be Sin[2t]:
coordinate to be Sin[2t]:
| ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax}] | |
make a parametric plot of a three‐dimensional curve | |
| ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax},{u,umin,umax}] | |
make a parametric plot of a three‐dimensional surface | |
| ParametricPlot3D[{{fx,fy,fz},{gx,gy,gz},…},…] | |
plot several objects together | |
ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax}] is the direct analog in three dimensions of ParametricPlot[{fx,fy},{t,tmin,tmax}] in two dimensions. In both cases, the Wolfram Language effectively generates a sequence of points by varying the parameter t, then forms a curve by joining these points. With ParametricPlot, the curve is in two dimensions; with ParametricPlot3D, it is in three dimensions.
This makes a parametric plot of a helical curve. Varying t produces circular motion in the  -
-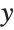 plane, and linear motion in the
plane, and linear motion in the 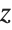 direction:
direction:
ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax},{u,umin,umax}] creates a surface, rather than a curve. The surface is formed from a collection of quadrilaterals. The corners of the quadrilaterals have coordinates corresponding to the values of the fi when t and u take on values in a regular grid.
Here the  and
and 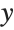 coordinates for the quadrilaterals are given simply by t and u. The result is a surface plot of the kind that can be produced by Plot3D:
coordinates for the quadrilaterals are given simply by t and u. The result is a surface plot of the kind that can be produced by Plot3D:
This shows the same surface as before, but with the 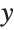 coordinates distorted by a quadratic transformation:
coordinates distorted by a quadratic transformation:
This produces a helicoid surface by taking the helical curve shown above, and at each section of the curve drawing a quadrilateral:
In general, it is possible to construct many complicated surfaces using ParametricPlot3D. In each case, you can think of the surfaces as being formed by "distorting" or "rolling up" the 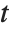 -
-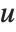 coordinate grid in a certain way.
coordinate grid in a certain way.
This produces a cylinder. Varying the t parameter yields a circle in the  -
-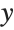 plane, while varying u moves the circles in the
plane, while varying u moves the circles in the 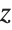 direction:
direction:
This produces a torus. Varying u yields a circle, while varying t rotates the circle around the 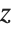 axis to form the torus:
axis to form the torus:
You should realize that when you draw surfaces with ParametricPlot3D, the exact choice of parametrization is often crucial. You should be careful, for example, to avoid parametrizations in which all or part of your surface is covered more than once. Such multiple coverings often lead to discontinuities in the mesh drawn on the surface, and may make ParametricPlot3D take much longer to render the surface.
As discussed in "The Structure of Graphics and Sound", the Wolfram Language includes a full graphics programming language. In this language, you can set up many different kinds of plots.
| LogPlot[f,{x,xmin,xmax}] | generate a linear-log plot |
| LogLinearPlot[f,{x,xmin,xmax}] | generate a log-linear plot |
| LogLogPlot[f,{x,xmin,xmax}] | generate a log-log plot |
| ListLogPlot[list] | generate a linear-log plot from a list of data |
| ListLogLinearPlot[list] | generate a log-linear plot from a list of data |
| ListLogLogPlot[list] | generate a log-log plot from a list of data |
| DateListPlot[list] | generate a plot from a list of data with date coordinates |
| DateListLogPlot[list] | generate a linear-log plot from a list of data with date coordinates |
| PolarPlot[r,{t,tmin,tmax}] | generate a polar plot of the radius r as a function of angle t |
| SphericalPlot3D[r,{theta,min,max},{phi,min,max}] | |
generate a three-dimensional spherical plot | |
| RevolutionPlot3D[f,{t,tmin,tmax}] | generate a three-dimensional surface of revolution |
| BarChart[list] | plot a list of data as a bar chart |
| PieChart[list] | plot a list of data as a pie chart |
Some of the plotting functions available are defined in the Standard Extra Packages included with the Wolfram System.
| ErrorListPlot[{{x1,y1,dy1},…}] | generate a plot with error bars |
| BoxWhiskerPlot[list] | generate a box-and-whisker plot of data |
| ParetoPlot[list] | generate a Pareto plot of data |
| PairwiseScatterPlot[data] | plot pairs of coordinates for multivariate data |
PairwiseScatterPlot can be used to plot pairs of columns from trivariate data:
Sound Playback
On most computer systems, the Wolfram System can produce not only graphics but also sound. The Wolfram System treats graphics and sound in a closely analogous way.
For example, just as you can use Plot[f,{x,xmin,xmax}] to plot a function, so also you can use Play[f,{t,0,tmax}] to “play” a function. Play takes the function to define the waveform for a sound: the values of the function give the amplitude of the sound as a function of time.
| Play[f,{t,0,tmax}] | play a sound with amplitude f as a function of time t in seconds |
Sounds produced by Play can have any waveform. They do not, for example, have to consist of a collection of harmonic pieces. In general, the amplitude function you give to Play specifies the instantaneous signal associated with the sound. This signal is typically converted to a voltage, and ultimately to a displacement. Note that amplitude is sometimes defined to be the peak signal associated with a sound; in the Wolfram System, it is always the instantaneous signal as a function of time.
Play is set up so that the time variable that appears in it is always measured in absolute seconds. When a sound is actually played, its amplitude is sampled a certain number of times every second. You can specify the sample rate by setting the option SampleRate.
| Play[f,{t,0,tmax},SampleRate->r] | play a sound, sampling it r times a second |
In general, the higher the sample rate, the better high‐frequency components in the sound will be rendered. A sample rate of r typically allows frequencies up to 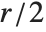 hertz. The human auditory system can typically perceive sounds in the frequency range 20 to 22000 hertz (depending somewhat on age and sex). The fundamental frequencies for the 88 notes on a piano range from 27.5 to 4186 hertz.
hertz. The human auditory system can typically perceive sounds in the frequency range 20 to 22000 hertz (depending somewhat on age and sex). The fundamental frequencies for the 88 notes on a piano range from 27.5 to 4186 hertz.
The standard sample rate used for compact disc players is 44100. The effective sample rate in a typical telephone system is around 8000. On most computer systems, the default sample rate used by the Wolfram System is around 8000.
You can use Play[{f1,f2,…}] to produce stereo sound. In general, the Wolfram System supports any number of sound channels.
| ListPlay[{a1,a2,…},SampleRate->r] | play a sound with a sequence of amplitude levels |
The function ListPlay allows you simply to give a list of values which are taken to be sound amplitudes sampled at a certain rate.
When sounds are actually rendered by the Wolfram System, only a certain range of amplitudes is allowed. The option PlayRange in Play and ListPlay specifies how the amplitudes you give should be scaled to fit in the allowed range. The settings for this option are analogous to those for the PlotRange graphics option discussed in "Options for Graphics".
| PlayRange->Automatic | use an internal procedure to scale amplitudes |
| PlayRange->All | scale so that all amplitudes fit in the allowed range |
| PlayRange->{amin,amax} | make amplitudes between amin and amax fit in the allowed range, and clip others |
While it is often convenient to use the setting PlayRange->Automatic, you should realize that Play may run significantly faster if you give an explicit PlayRange specification, so it does not have to derive one.
| EmitSound[snd] | emit a sound when evaluated |
A Sound object in output is typically formatted as a button which contains a visualization of the sound and which plays the sound when pressed. Sounds can be played without the need for user intervention or producing output by using EmitSound. In fact, the internal implementation of Sound buttons uses EmitSound when the button is pressed.