



PolarPlot
Details and Options




- The angle
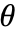 is measured in radians, counterclockwise from the positive
is measured in radians, counterclockwise from the positive 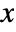 axis.
axis. - The
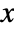 ,
, 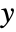 position corresponding to
position corresponding to 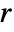 ,
, 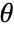 is
is 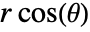 ,
, 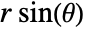 . The value of
. The value of 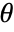 need not be between
need not be between 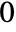 and
and 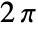 .
. - PolarPlot treats the variable
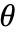 as local, effectively using Block.
as local, effectively using Block. - PolarPlot has attribute HoldAll and evaluates functions only after assigning specific numerical values to
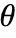 .
. - In some cases, it may be more efficient to use Evaluate to evaluate functions symbolically before specific numerical values are assigned to
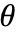 .
. - No curve is drawn in any region where a function evaluates to None.
- The following wrappers w can be used for r:
-
Annotation[r,label] provide an annotation for r Button[r,action] evaluate action when the curve for r is clicked Callout[r,label] label the function with a callout Callout[r,label,pos] place the callout at relative position pos EventHandler[r,events] define a general event handler for r Hyperlink[r,uri] make the function a hyperlink Labeled[r,label] label the function Labeled[r,label,pos] place the label at relative position pos Legended[r,label] identify the function in a legend PopupWindow[r,cont] attach a popup window to the function StatusArea[r,label] display in the status area on mouseover Style[r,styles] show the function using the specified styles Tooltip[r,label] attach a tooltip to the function Tooltip[r] use functions as tooltips - Wrappers w can be applied at multiple levels:
-
w[r] wrap r w[{r1,r2,…}] wrap a collection of curves w1[w2[…]] use nested wrappers - Callout, Labeled and Placed can use the following positions pos:
-
Automatic automatically placed labels Above, Below, Before, After positions around the curve u near the curve at parameter u {x,y} position near {x,y} Scaled[s] scaled position s along the curve {s,Above},{s,Below},… relative position at position s along the curve {pos,epos} epos in label placed at relative position pos of the curve - PolarPlot has the same options as Graphics, with the following additions and changes: [List of all options]
-
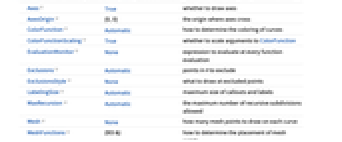
Axes True whether to draw axes AxesOrigin {0,0} the origin where axes cross ColorFunction Automatic how to determine the coloring of curves ColorFunctionScaling True whether to scale arguments to ColorFunction EvaluationMonitor None expression to evaluate at every function evaluation Exclusions Automatic points in 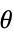 to exclude
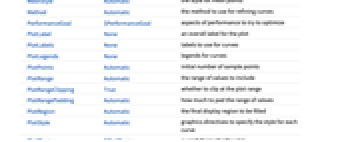
to excludeExclusionsStyle None what to draw at excluded points LabelingSize Automatic maximum size of callouts and labels MaxRecursion Automatic the maximum number of recursive subdivisions allowed Mesh None how many mesh points to draw on each curve MeshFunctions {#3&} how to determine the placement of mesh points MeshShading None how to shade regions between mesh points MeshStyle Automatic the style for mesh points Method Automatic the method to use for refining curves PerformanceGoal $PerformanceGoal aspects of performance to try to optimize PlotLabels None labels to use for curves PlotLegends None legends for curves PlotPoints Automatic initial number of sample points PlotRange Automatic the range of values to include PlotRangeClipping True whether to clip at the plot range PlotStyle Automatic graphics directives to specify the style for each curve PlotTheme $PlotTheme overall theme for the plot PolarAxes False whether to draw polar axes PolarAxesOrigin Automatic where to draw polar axes PolarGridLines None polar gridlines to draw PolarTicks Automatic polar axes ticks RegionFunction (True&) how to determine whether a point should be included ScalingFunctions None how to scale individual coordinates WorkingPrecision MachinePrecision the precision used in internal computations - Typical settings for PlotLegends include:
-
None no legend Automatic automatically determine legend "Expressions" use r1, r2, … as legend labels {lbl1,lbl2,…} use lbl1, lbl2, … as legend labels Placed[lspec,…] specify placement for legend - ColorData["DefaultPlotColors"] gives the default sequence of colors used by PlotStyle.
- PolarPlot initially evaluates functions at a number of equally spaced sample points specified by PlotPoints. Then it uses an adaptive algorithm to choose additional sample points, subdividing a given interval at most MaxRecursion times.
- You should realize that with the finite number of sample points used, it is possible for PolarPlot to miss features in your function. To check your results, you should try increasing the settings for PlotPoints and MaxRecursion.
- On[PolarPlot::accbend] makes PolarPlot print a message if it is unable to reach a certain smoothness of curve.
- With Mesh->All, PolarPlot will explicitly draw a point at every position on each curve where each function was sampled.
- The arguments supplied to functions in MeshFunctions and RegionFunction are x, y, θ, r. Functions in ColorFunction are by default supplied with scaled versions of these arguments.
- The functions are evaluated all along each curve.
- With the default settings Exclusions->Automatic and ExclusionsStyle->None, PolarPlot breaks curves at discontinuities it detects. Exclusions->None joins across discontinuities.
- PolarPlot normally returns Graphics[{Line[…],…}].
- Possible settings for ScalingFunctions include:
-
sr scale the r axis {sx,sy,sθ,sr} scale x, y, θ and r - Common built-in scaling functions s include:
-
"Log" 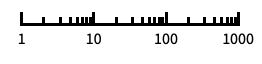
log scale with automatic tick labeling "Log10" 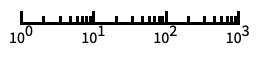
base-10 log scale with powers of 10 for ticks "SignedLog" 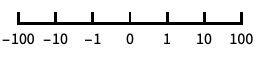
log-like scale that includes 0 and negative numbers "Reverse" 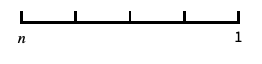
reverse the coordinate direction - Scaling θ affects how the plot is sampled, but not the overall appearance of the plot.
- In general, you cannot scale both x or y and r simultaneously.
-
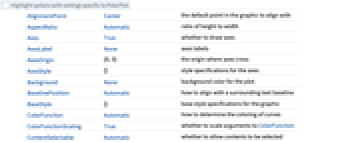
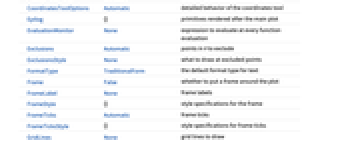
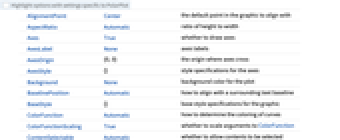
AlignmentPoint Center the default point in the graphic to align with AspectRatio Automatic ratio of height to width Axes True whether to draw axes AxesLabel None axes labels AxesOrigin {0,0} the origin where axes cross AxesStyle {} style specifications for the axes Background None background color for the plot BaselinePosition Automatic how to align with a surrounding text baseline BaseStyle {} base style specifications for the graphic ColorFunction Automatic how to determine the coloring of curves ColorFunctionScaling True whether to scale arguments to ColorFunction ContentSelectable Automatic whether to allow contents to be selected CoordinatesToolOptions Automatic detailed behavior of the coordinates tool Epilog {} primitives rendered after the main plot EvaluationMonitor None expression to evaluate at every function evaluation Exclusions Automatic points in 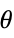 to exclude
to excludeExclusionsStyle None what to draw at excluded points FormatType TraditionalForm the default format type for text Frame False whether to put a frame around the plot FrameLabel None frame labels FrameStyle {} style specifications for the frame FrameTicks Automatic frame ticks FrameTicksStyle {} style specifications for frame ticks GridLines None grid lines to draw GridLinesStyle {} style specifications for grid lines ImageMargins 0. the margins to leave around the graphic ImagePadding All what extra padding to allow for labels etc. ImageSize Automatic the absolute size at which to render the graphic LabelingSize Automatic maximum size of callouts and labels LabelStyle {} style specifications for labels MaxRecursion Automatic the maximum number of recursive subdivisions allowed Mesh None how many mesh points to draw on each curve MeshFunctions {#3&} how to determine the placement of mesh points MeshShading None how to shade regions between mesh points MeshStyle Automatic the style for mesh points Method Automatic the method to use for refining curves PerformanceGoal $PerformanceGoal aspects of performance to try to optimize PlotLabel None an overall label for the plot PlotLabels None labels to use for curves PlotLegends None legends for curves PlotPoints Automatic initial number of sample points PlotRange Automatic the range of values to include PlotRangeClipping True whether to clip at the plot range PlotRangePadding Automatic how much to pad the range of values PlotRegion Automatic the final display region to be filled PlotStyle Automatic graphics directives to specify the style for each curve PlotTheme $PlotTheme overall theme for the plot PolarAxes False whether to draw polar axes PolarAxesOrigin Automatic where to draw polar axes PolarGridLines None polar gridlines to draw PolarTicks Automatic polar axes ticks PreserveImageOptions Automatic whether to preserve image options when displaying new versions of the same graphic Prolog {} primitives rendered before the main plot RegionFunction (True&) how to determine whether a point should be included RotateLabel True whether to rotate y labels on the frame ScalingFunctions None how to scale individual coordinates Ticks Automatic axes ticks TicksStyle {} style specifications for axes ticks WorkingPrecision MachinePrecision the precision used in internal computations
List of all options



Examples
open all close allScope (23)
Sampling (6)
More points are sampled when the function changes quickly:
The plot range is selected automatically:
Ranges where the function becomes nonreal are excluded:
The curve is split when there are discontinuities in the function:
Use PlotPoints and MaxRecursion to control adaptive sampling:
Use PlotRange to focus in on areas of interest:
Labeling and Legending (7)
Use Callout to add the expressions as a label:
Place the label along the curve:
Place the label at a scaled position:
Place the labels relative to the inside of the curve:
Place the labels relative to the outside of the curve:
Label the curve with PlotLabels:
Presentation (10)
Multiple curves are automatically colored to be distinct:
Provide explicit styling to different curves and regions:
Provide an interactive Tooltip for each curve:
Style the areas between mesh levels:
Use a theme with dark background and high-contrast colors:
Use a theme with minimal styling:
Options (134)
AspectRatio (3)
By default, the ratio of the height to width for the plot is determined automatically:
Make the height the same as the width with AspectRatio1:
AspectRatioFull adjusts the height and width to tightly fit inside other constructs:
Axes (4)
Use AxesFalse to turn off axes:
Use AxesOrigin to specify where the axes intersect:
AxesOrigin (2)
AxesStyle (4)
ColorFunction (4)
Color the curve by scaled ![]() ,
, ![]() ,
, ![]() , or
, or ![]() value:
value:
ColorFunction has higher priority than PlotStyle:
EvaluationMonitor (3)
Exclusions (3)
ExclusionsStyle (2)
Frame (4)
FrameLabel (3)
FrameTicks (8)
Frame ticks are placed automatically by default:
Use frame ticks on the bottom edge:
By default, the top and right edges have tick marks but no tick labels:
Use All to include tick labels on all edges:
Place tick marks at specific positions:
Draw frame tick marks at the specified positions with specific labels:
Specify the lengths for tick marks as a fraction of the graphics size:
Use different sizes in the positive and negative directions for each tick mark:
FrameTicksStyle (3)
ImageSize (7)
Use named sizes such as Tiny, Small, Medium and Large:
Specify the width of the plot:
Specify the height of the plot:
Allow the width and height to be up to a certain size:
Specify the width and height for a graphic, padding with space if necessary:
Setting AspectRatioFull will fill the available space:
Use maximum sizes for the width and height:
Use ImageSizeFull to fill the available space in an object:
Specify the image size as a fraction of the available space:
LabelingSize (2)
MaxRecursion (1)
Each level of MaxRecursion will adaptively subdivide the initial mesh into a finer mesh:
Mesh (4)
MeshFunctions (2)
MeshShading (6)
Alternate red and blue arcs in the ![]() direction:
direction:
Use None to remove segments:
MeshShading can be used with PlotStyle:
MeshShading has higher priority than PlotStyle for styling:
Use PlotStyle for some segments by setting MeshShading to Automatic:
MeshShading can be used with ColorFunction:
MeshStyle (4)
PerformanceGoal (2)
PlotLabels (6)
PlotLabels->"Expressions" uses functions as curve labels:
Specify the text to label the curves:
Place the labels above the curves:
Place the labels differently for each curve:
Use callouts to identify the curves:
Put labels relative to the outside of the curves:
Use None to not add a label:
PlotLegends (7)
No legends are used by default:
PlotLegends automatically picks up PlotStyle option values:
Show expressions as legends in TraditionalForm:
Specify a list of labels for legends:
Legend layout changes automatically along with position:
Use LineLegend to adjust the appearance of the legend:
Specify LegendMarkers:
PlotRange (2)
With the natural range of values, the fine detail around the origin is not visible:
Use PlotRange to focus in on areas of interest:
PlotStyle (5)
Use different style directives:
By default, different styles are chosen for multiple curves and regions:
Explicitly specify the style for different curves and regions:
PlotStyle can be combined with ColorFunction:
PlotStyle can be combined with MeshShading:
PlotTheme (1)
PolarAxesOrigin (2)
PolarGridLines (3)
PolarTicks (3)
ScalingFunctions (8)
By default, PolarPlot uses natural scale in both axes:
Log-scaled plots will only plot intervals over which Log is defined:
Use a shifted log scale to show a function with negative values:
Use ScalingFunctions to reverse the coordinate direction in the ![]() direction:
direction:
Use a reciprocal scale in the ![]() direction:
direction:
Use a scale defined by a function and its inverse:
Use a scale for θ; it affects how the plot is sampled, but not the overall appearance of the plot:
Ticks (9)
Ticks are placed automatically in each plot:
Use TicksNone to draw axes without any tick marks:
Use ticks on the ![]() axis, but not the
axis, but not the ![]() axis:
axis:
Place tick marks at specific positions:
Draw tick marks at the specified positions with specific labels:
Use specific ticks on one axis and automatic ticks on the other:
Specify the lengths for ticks as a fraction on graphics size:
Use different sizes in the positive and negative directions for each tick:
Specify a style for each tick:
Construct a function that places ticks at the midpoint and extremes of the axis:
TicksStyle (4)
Applications (4)
An oscillation around a circle:
Archimedean spirals of the form ![]() :
:
Archimedean spirals of the form ![]() :
:
Logarithmic spirals have the form ![]() :
:
Create a Guilloché pattern [more info]:
Properties & Relations (5)
PolarPlot is a special case of ParametricPlot for curves:
Use ListPolarPlot for data:
Use Plot3D and ParametricPlot3D for function and parametric surfaces:
Use RevolutionPlot3D and SphericalPlot3D for cylindrical and spherical coordinates:
Use ContourPlot and RegionPlot for implicit curves and regions:
Tech Notes
Related Guides
History
Introduced in 2007 (6.0) | Updated in 2008 (7.0) ▪ 2012 (9.0) ▪ 2014 (10.0) ▪ 2019 (12.0) ▪ 2022 (13.1)
Text
Wolfram Research (2007), PolarPlot, Wolfram Language function, https://reference.wolfram.com/language/ref/PolarPlot.html (updated 2022).
CMS
Wolfram Language. 2007. "PolarPlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/PolarPlot.html.
APA
Wolfram Language. (2007). PolarPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PolarPlot.html
BibTeX
@misc{reference.wolfram_2025_polarplot, author="Wolfram Research", title="{PolarPlot}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/PolarPlot.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_polarplot, organization={Wolfram Research}, title={PolarPlot}, year={2022}, url={https://reference.wolfram.com/language/ref/PolarPlot.html}, note=[Accessed: 24-February-2026]}