Filling

Filling

is an option for ListPlot, Plot, Plot3D, and related functions that specifies what filling to add under points, curves, and surfaces.

Details

  • The following settings can be used:
  • Noneno filling (default)
    Axisfill to the axis
    Bottomfill to the bottom of the plot
    Topfill to the top of the plot
    vfill to value v
    {m}fill to the m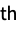^(th) object
    {i1->p1,i2->p2,…}fill from object ik to pk
    {i1->{p1,g1},…}use directive gk for the k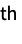^(th) filling
    {i1->{p1,{g1-,g1+},…}}use g1- below and g1+ above
  • For 2D graphics, filling is done in the y direction.
  • For 3D graphics, filling is done in the z direction, and on the bounding xy plane.
  • In ListPlot, filling effectively draws a "stem" to every point.
  • For multiple curves, surfaces or lists of points, Filling->p is equivalent to Filling->{1->p,2->p…}.
  • In filling between lists of points that do not line up, the "stems" start at points in the first list, and extend to positions that linearly interpolate between points in the second list.
  • By default, the style specified by the setting for FillingStyle is used for all filling.
  • Settings of the form ik->{pk,gk} can be used to override the default in particular cases.
  • ik->{pk,{gk -,gk +}} specifies that style gk - should be used when ik lies below pk, and gk + when it lies above.
  • The gk - and gk + can be composite directives specified with Directive.

Examples

open allclose all

Basic Examples  (4)

Fill to different levels:

Fill multiple curves:

Fill for a point-oriented plot:

Fill for a surface-oriented plot:

Scope  (14)

Filling Limits  (4)

Fill to different levels:

Overlapping fills by default combine using opacity:

Fill between curve 1 and the axis:

Fill between curves 1 and 2:

Filling Style  (7)

Fill between curves 1 and 2 with a specific style:

Fill between curves 1 and with yellow:

Fill between curves 1 and 2; use yellow when 1 is below 2, and green when 1 is above 2:

Use an overall FillingStyle specification:

Fill with opacity 0.5 orange:

Fill with orange below the axis, and yellow above:

Use a variable filling style obtained from a ColorFunction:

Plot Functions  (3)

Point-oriented plot functions will fill using a stem:

Line-oriented plot functions will fill using an area:

Surface-oriented plot functions will fill along the boundary:

Applications  (2)

Here styles indicate where the function differs from its step approximation:

Difference between the function and its linear approximation:

The Factorial function compared to an asymptotic expansion:

Neat Examples  (1)

Eigenfunctions in a potential well:

Wolfram Research (2007), Filling, Wolfram Language function, https://reference.wolfram.com/language/ref/Filling.html.

Text

Wolfram Research (2007), Filling, Wolfram Language function, https://reference.wolfram.com/language/ref/Filling.html.

CMS

Wolfram Language. 2007. "Filling." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Filling.html.

APA

Wolfram Language. (2007). Filling. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Filling.html

BibTeX

@misc{reference.wolfram_2024_filling, author="Wolfram Research", title="{Filling}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/Filling.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_filling, organization={Wolfram Research}, title={Filling}, year={2007}, url={https://reference.wolfram.com/language/ref/Filling.html}, note=[Accessed: 21-November-2024 ]}