WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター
音声の合成

音声の合成

振動過程と時系列
ノイズ生成高度な合成
Wolfram言語は，Wolfram言語のパワフルな数学およびアルゴリズム機能と完全に統合した，音声データの生成，解析，操作に対する広範なサポートを提供している．
音声合成に使う最初の関数としてAudioGeneratorがある．
AudioGenerator[model]
指定された model の1秒の音声を生成する
AudioGenerator[model,t]
t 秒の音声を生成する
音声の生成
振動
信号を生成する最も簡単な方法は，AudioGeneratorでサポートされるネイティブの振動の一つを使うことである．
正弦波信号を生成する：
指定した周波数の正弦波信号を生成する：
振動モデルによって，調和性も異なる：
振動モデルはすべて周波数と位相に対する，時間依存のパラメータを取る．入力には，TimeSeries，他のAudioオブジェクト，純関数が取れる．
音声信号を使って周波数を制御する：
純関数を使って周波数を制御する：
時系列を使って周波数を制御する：
ノイズ生成
AudioGeneratorは，振動器の他，異なる種類のノイズ信号の生成を可能にする．
ピンクのイズを1秒生成する：
ノイズのタイプによってスペクトルコンテンツも異なる：
ホワイトのイズは，平坦なスペクトルが特徴である．デフォルトではサンプル値は一様分布から選ばれるが，スペクトルに影響を及ぼさずに変更することができる．
正規分布からサンプルされた，振幅のあるホワイトノイズ：
信号のヒストグラムとピリオドグラムをプロットする：
{"Color",α}を使うと，f-α 分布に従うスペクトルを持つ，色付きのノイズ信号を生成することができる．色付きのノイズには"Pink"，"Brown"，"Blue"があり，ここで α は1，2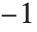，のいずれかである．
ノイズの「色」を変更する：
過程と時系列
AudioGeneratorを使うと，ランダム過程をサンプルすることで信号を生成することができる．
離散時間および連続時間の過程から音声信号を生成する：
AudioGeneratorはTimeSeriesからAudioオブジェクトを生成するためにも使うことができる．
TimeSeriesから始まる音声信号を生成する：
高度な合成

減算合成

音声オブジェクトを1つ以上の周波数選択フィルタで処理することにより，その調和性を操作することができるため，音色が変わる．この方法は，もとの音声オブジェクトが調和的に豊かな場合に効果的である．
のこぎり波のフィルタを適用する：
2つの異なるフィルタを使って，矩形波形を生成する：

加算合成

フィルタに使用で調和が減衰する減算合成とは対照的に，加算合成は調波を加えることに基づいている．その効果は，異なる周波数における正弦波の線形結合により得られる．ユーザは線形結合の係数を制御することができる．
基音200 Hzの最初の8個の調音の振幅を制御する：

振幅変調

振幅変調は，複雑な調和性を持つ信号を生成する一般的な手法である．
振幅変調では，carrier（搬送波）とmodulator（変調波）の2つの信号が使われる．結果は carrier(1+μmodulator)で計算される．ここでスケール係数 μ は変調度と呼ばれる．
変調波が正弦波の場合は，周波数 f の搬送波の各コンポーネントについて，1対の側波帯が周波数 f±m で生成され，その振幅は変調度によって制御される．
三角波の振幅変調：
信号のピリオドグラムをプロットする：

周波数変調

よく使われる別の方法として，1970年代の初期に発見された周波数変調というものがある．
周波数変調の場合，搬送波の周波数は変調波および変調度によって制御される．変調度が増加するにつれて，変調周波数の区間における搬送波周波数の上か下で周波数が発生する．
基本的な周波数変調：
信号のピリオドグラムをプロットする：
これらの追加的な側波帯の数と強さは，変調度が関連している．
変調指数の大きさを上げると，側波帯の大きさが増加する：
側波帯の位置は搬送波と変調周波数の間の割合で決まる．この割合を変更することで， 調和スペクトル（音程のある楽器に特有）と非調和スペクトル（打楽器に特有）の両方を得ることができる．
調和信号と非調和信号を生成する：
変調度が時間依存の引数になると，調和性が時間とともに進化する信号が簡単に生成できるようになる．
変調度を大きくして，信号のバンド幅を増加させる：
結果のスペクトログラムをプロットする：
変調周波数は時間依存のパラメータでもよい．
変調周波数を変化させて，側波帯の位置を変更する：
結果のスペクトログラムをプロットする：