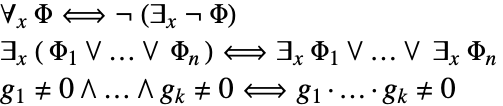はじめに

Wolfram言語関数のReduce，Resolve，FindInstanceを使うと，方程式および不等式で表すことのできる広範な問題を解くことができる．これらの関数では，与えられた問題を，アルゴリズムで解くことのできる問題の列に還元しようと試みるヒューリスティックが使われる．この他にも，特別の性質を満足するクラスの問題に適用可能な多数のアルゴリズムが使われる．このドキュメントでは，複素多項式系として知られる問題のクラスを解くのに使われるアルゴリズムを説明する．また，返された答の構造の特徴を示し，複素多項式系を解く際にさまざまな面で影響を及ぼすオプションについて述べる．

複素多項式系とは，整方程式と不等式で構築された式

を，下のように論理結合子および量限定子を使って結合したものである．

変数 がまたは内に現れることを束縛出現， がその他の部分に現れることを自由出現という．複素多項式系に変数 の自由出現がある場合， はその系の自由変数という．複素多項式系に量限定子が含まれない場合は，quantifier-freeという．

以下は，自由変数，， を持つ複素多項式系の例である．

Wolfram言語では量限定子は，関数Exists ()およびForAll ()を使って表す．

複素多項式系はすべて，次のような冠頭標準形

に変換することができる．ここで，それぞれの は量限定子またはであり，はquantifier-freeである．

quantifier-freeの複素多項式系はすべて，選言標準形に変換することができる．

ここで，それぞれの は整方程式あるいは不等式である．

Reduce，Resolve，FindInstanceは常に複素多項式系を冠頭標準形に，そのquantifier-free部を選言標準形にし，方程式と不等式の両辺を減算して以下の形式にする．

以下のセクションでは，常に系がこの形式に変換されたものと想定する．

Reduce を使うと，任意の複素多項式系を解くことができる．解（についてを拡張した後）は項の選言で，以下の形式となる．

ここで は系の自由変数，各 は多項式，各 は根号かRootオブジェクトを使って表される代数関数であり，連言項(2)はない可能性がある．各 は正しく定義されている．つまり， の分母およびRootオブジェクトの主要項は，連言(2)に先行する項を満足するいかなるについてもゼロにならないということである．

Resolveは任意の複素多項式系から量限定子を除去することができる．変数が指定されていなければ，結果は次の項

の論理結合となる（ここで と は多項式，各 は系の自由変数である）．入力で変数が指定されていれば，ResolveはReduceと同じ答を与える．

FindInstanceは任意の複素多項式系を扱うことができ，複素数解の例，あるいは空リスト（系に解がない場合）を与える．複数の例が要求された場合，例は系のすべての解からランダムに生成されるので，RandomSeedオプションの値に依存する可能性がある．1つの例が要求された場合は，1つの例だけを生成するより高速なアルゴリズムが使われ，返される例は常に同じものになる．

複素多項式系を解くときに使われる主なツールは，グレブナー基底アルゴリズム[1]である．これはWolfram言語ではGroebnerBasis関数として直接利用することができる．

グレブナー基底

理論

このセクションでは，グレブナー基底の理論を簡単に紹介する．ここでは，Wolfram言語で複素多項式系を解く場合に使用されるアルゴリズムを説明するのに必要な性質だけを提示する．詳細は[1, 2]等を参照のこと．[2]でmonomial（単項式）と呼ばれているものは，[1]ではterm（項），またその逆となっている点に注意する．このドキュメントでは[1]で使われている用語を使用する．

中の単項式は，非負の整数 を持つ形式 の式である．

ここで，は の単項式すべての集合であるとする．単項式順序は 上では線形順序であり，すべての について となる． はすべての について となることを示す．

が体，整数領域，体上の一変数多項式の領域のいずれかであるとする．また， と が次のように定義される関数 であるとする．その定義とは「 が体であれば， で となる． が整数領域であれば， および は整数商との剰余関数である． が，体の一変数多項式の領域であれば， および は多項商と剰余関数である」というものである．

が の非零要素で が単項式であるときの積 は項と呼ばれる．

上の単項式順序を として，とする． の先頭単項式 は- で現れる最大の単項式， の主係数 は の での係数であり， の先頭項 は積 となる．

単項式順序では，のイデアル のグレブナー基底は，多項式の有限集合 である．ここでは， のそれぞれについて，が で割り切れるような が存在する．すべてのイデアル はグレブナー基底を持つ（証明は[1]等を参照のこと）．

として，が単項式だとしよう． が で割り切れ，ならば，項 は を法として可約である． が を法として可約ならば， を法とする の簡約化は多項式

となる．ここで ならば となり，それ以外の場合は となる点に注意する．

で， が の順序付き有限部分集合であるとする． に の要素を法として可約な項が含まれていれば， は を法として可約である． を法とした の簡約化 は次の手順で定義される． の要素を法として可約な の項の集合 が空集合でないときに，-最大の単項式を持つ項 を取り， が を法として可約であるような最初の を取り， の項 を で置換するのである．この手順の後続するステップで選ばれる項 の単項式は，-降鎖を形成し，各単項式は最大 回現れる．ここで は の要素数であるため，手順は終了する．

グレブナー基底 は，すべての について が を法として可約ではなく，かつ， が整数領域 である場合，半簡約化されているという．

Wolfram言語関数のGroebnerBasisは半簡約化されたグレブナー基底を返す．以下の説明では，グレブナー基底はすべて半簡約化されたものと仮定する．ここでは，基底多項式はモニックである必要はないので，文献で定義されている既約グレブナー基底と同じものではない．単項式順序が固定されているときは，各イデアルが一意の既約グレブナー基底を持つ．ここで定義する半簡約化されたグレブナー基底は， の可逆元による乗算までしか一意ではない（性質 2を参照のこと）．

性質 1：のイデアル のグレブナー基底を とし，とする．この場合，のとき，かつそのときに限り である．

これは，定義の簡単な結果として成り立つ．

性質 2：同じ単項式順序でのイデアル の2つのグレブナー基底を および とする．また， と の要素が先頭単項式によって順序付けられているとする．この場合， となり， が整数領域の場合はすべての について となる．それ以外の場合は の任意の逆元 について となる．

証明：ならば，が を法として可約であるか，が を法として可約であるかのどちらかとなる．よって，グレブナー基底の要素の先頭単項式はすべて異なる．一般性を失わずに と仮定する．帰納法を使うために， と固定し，すべての について， の可逆元 については であると仮定する． が整数領域ならば，である．一般性を失わずに と仮定する． は に属しているので，が で割り切れるような が存在する．よって で， となる． ならば， は を法として可約である．また，ここで を法とすることもできそうであるが，これはありえない．なぜならば， が半簡約化されているからである．従って，，であり，は で割り切れる．同様に は で割り切れる．よって，となるような の可逆元 が存在する． が整数領域ならば，と は正となり，となる． としてみよう．ここで であると仮定する． は に属するので，一部の については で割り切れなければならない． と がそれぞれ における および の係数であるとする． が体であるなら， の項 は を法として可約である．これは が半簡約化されているという仮定に反する． が体の一変数多項式の領域ならば，

であるので， が を法として可約であるか， が を法として可約であるかのどちらかとなる．しかし，後者は と が半簡約化されているという前提に反する．最後に を整数領域とする． は を法として可約ではなく， も を法として可約ではないので，およびとなる．は で割り切れるので，は不可能である．従って が成り立つので， となる． についての帰納法により，すべての について が成り立つ． ならば，は （このとき ）を法として可約であり，は を法として可約である．よって， となり，性質 2が証明される．

性質 3： が のイデアルで，であり， が のイデアル のグレブナー基底であるとする．この場合， の可逆元 について が成り立つとき，かつそのときに限り は の基底になる．

イデアルに の可逆元が含まれるなら，GroebnerBasisは常にを返す．

証明：まず，

は，任意の非負の整数 のときイデアル に属す．ゆえに， が の基底に属していれば，1は に属す． は のグレブナー基底なので，要素 の主係数は1を割り切るようなものでなければならない．ゆえに は の可逆元である． は半簡約化されており，どの項も で割り切れるので，となる．ここで の可逆元 について であると仮定する．1は に属するので，

が成り立つ．ここで各 は に属し，各 は に属す． のベキ乗での係数を比較することで， を法とする方程式 ，（のとき），が導かれる．次に，（のとき）， を法とする という方程式になる．従って， は の基底に属す．これで性質 3が証明される．

さらに技術的な以下の性質は，複素多項式系を解く際に重要である．

性質 4： を含む単項式が を含まないものよりも大きくなるような単項式順序でののイデアル のグレブナー基底を とする．また， について最小の正の次数 を持つ の要素を ， についての の主係数を ， に依存しない の要素すべてをとする．ここで，任意の多項式 および点について，，（ のとき），ならば，である．

証明： を で割ったときの擬剰余 を の多項式と考える．

と は に属すので， も に属す．性質 1により， による の簡約はゼロでなければならない． についての の次数は よりも小さいので， は に依存する のどの要素によっても簡約されない．そこで

が成り立ち，も成り立つ．なので，(1)は であることを示しており，これで性質 4が証明される．

Wolfram言語関数のGroebnerBasis

Wolfram言語関数のGroebnerBasisは，半簡約化されたグレブナー基底を求める．このセクションでは，複素多項式系の解法で使用されるGroebnerBasisのオプションを説明する．

複素多項式系の解法で使われるGroebnerBasisのオプション

CoefficientDomain

このオプションは係数の領域 を指定する．デフォルトのAutomatic設定では，係数領域は入力に存在する数値係数によって生成された体になる．

Integers	整数領域
InexactNumbers[prec]	精度 prec の非厳密数
Polynomials[x]	の多項式領域
RationalFunctions	GroebnerBasisに与えられた変数リストにはない変数の有理関数体
Rationals	有理数体

CoefficientDomainで使える設定

係数領域 もGroebnerBasisのModulusオプションの設定に依存する．Modulus->pという設定では，素数 についての係数領域は体 ，また，CoefficientDomain->RationalFunctionsのときは 上の有理関数体となる．

Method

デフォルト設定のMethod->Automaticでは，GroebnerBasisでBuchbergerアルゴリズムの変形が使われる．この他に使えるアルゴリズムはグレブナーウォークで，グレブナー基底をより簡単な単項式順序で計算してから，要求される難しい単項式順序に変換するものである．これは，要求された順序で直接グレブナー基底を計算するよりも速いことが多い．特に入力の多項式が簡単な順序のグレブナー基底であることが分かっている場合に有効である．設定Method->AutomaticではGroebnerBasisでデフォルトのCoefficientDomain->RationalsおよびMonomialOrder->Lexicographicのグレブナーウォークが使われる．

グレブナーウォーク法を使ったグレブナー基底の変換

MonomialOrder

このオプションは，単項式順序を指定する．値は指定された単項式順序のいずれか，あるいは重み行列のどちらかである．以下の表は となる条件を与える．

Lexicographic
DegreeLexicographic
DegreeReverseLexicographic

単項式順序

QE(量限定子除去)では，量限定子変数を含む単項式が含まないものよりも大きくなるような順序が必要である．Lexicographic順序はこの条件を満足するが，次のEliminationOrderの方が通常計算が速い．

ここで は合計次数， は自由変数， は量限定子変数， と は単項式，はDegreeReverseLexicographic順序を表している．

EliminationOrderを使うときは，除去変数を指定したGroebnerBasisシンタックスが必要である．

除去順序におけるグレブナー基底

MonomialOrder->EliminationOrderと設定されているGroebnerBasisでは，デフォルトで を含む多項式を結果から削除し， の基底多項式だけを返す．基底多項式をすべて得るためには，GroebnerBasisOptionsグループのシステムオプションEliminateFromGroebnerBasisの値を変更しなければならない（Wolfram言語はQE法でこのオプションを局所的に変更する）．オプション値は以下のように変更することができる．

SetSystemOptions["GroebnerBasisOptions"->{"EliminateFromGroebnerBasis"->False}].

システムオプションEliminateFromGroebnerBasis

以下によりから が除去される．答となる多項式は，その零点が，もとの2つの方程式の解集合を平面上に投影したときのZariski閉包となるようなものである：

解集合を平面上へ投影したときの厳密な記述は，すべての基底多項式に依存する．あるいは がゼロのときは，2番目の基底多項式はゼロにはならないことに注意する：

Resolveにより平面上への解集合の投影の正確な記述が得られる：

決定問題

決定問題とは，すべての変数が存在量化された系である．つまり，以下の形式の系のことである．

ここで はすべての変数となっている．決定問題を解くことは，それがTrueとFalseのどちらと等価であるかを判定すること，言い換えれば，量限定子を含まない整方程式および不等式の系が解を持つかどうかを判定することである．

以下の恒等式

を仮定すると，いかなる決定問題を解くことも，以下の形式の有限個の決定問題を解くことに還元できる．

ヒルベルトの零点定理(Nullstellensatz)およびグレブナー基底の性質 3により，

は，任意の単項式順序の

が{1}と異なるとき，かつ，そのときに限り複素数解を持つ．

次は が複素数解を持つことを示している：

これは が複素数解を持たないことを示している：

Wolfram言語で決定問題を解く場合，GroebnerBasisの計算で使われる単項式順序は，{z}が除去変数リストとして指定されたMonomialOrder->EliminationOrderである．この設定は，zを含む単項式の方が，含まないものよりも大きくなるような単項式順序に相当し，zを含まない単項式の順序は次数逆辞書式順序になる．不等式条件がない場合は，zを導入する必要はなく，Wolfram言語はMonomialOrder->DegreeReverseLexicographicという設定を使う．

QE（量限定子除去）

複素多項式系にはどれも，それと等価のquantifier-freeの複素多項式系が存在する．このことは，半代数的構成可能集合（quantifier-freeの整方程式および不等式の系の解集合）の投影が，半代数的構成可能集合であるというシュヴァレー(Chevalley)の定理に従っている（[3]を参照）．QEは指定された複素多項式系と等価のquantifier-freeの複素多項式系を見付ける手続きである．Wolfram言語では，複素多項式系のQEはResolveで実行される．また，QEは複素多項式の解法もしくは解の例の探索の第一段階として，ReduceおよびFindInstanceでも使われる．

Wolfram言語では，複素多項式系に以下のようなQE法が使われる．例えば，次の恒等式があるとする．

どのような複素多項式系から量限定子を除去することも，下の系から単一の存在記号を有限回数除去することに還元される．

(1)から量限定子を除去するために，Wolfram言語ではまず， を含む単項式が を含まないものよりも大きくなるような単項式順序で，方程式のグレブナー基底

を計算する．

使用される単項式順序は，EliminationOrderである．ここでは除去変数リストで指定されており，すべての基底多項式は維持されている．

が に依存する多項式を含まないならば，(1)と等価のquantifier-freeの系は， のすべての要素をゼロとし， の多項式としての の係数の少なくとも1つがゼロではないとすることで得ることができる．これ以外の場合は， の最低の正の次数d を持つ の要素を とし， の の主係数を とし， に依存しない の要素すべてをとする．これで(1)は，2つの系の選言

および

に分割できる．(2)から量限定子を除去するために，QEが再帰的に呼び出される．で生成されるイデアルは，で生成されるイデアルを厳密に含んでいるので，多項式環がネーターであるという性質により，再帰が有限であると保証される．

がで生成されるイデアルの基底に属すなら（これは厳密に1が

に属すときである），(3)はFalseと等価になる．そうでない場合は， を で割ったときの擬剰余を の多項式として

とする．これで(3)はquantifier-freeの系

と等価になる．(3)が(4)を意味することを示すために，が(3)を満足すると仮定する．となり，

が成り立つような が存在する．および はで生成されるイデアルに属すので，

および が成り立つ．従って，

を示す

が成り立つ．(4)が(3)を意味することを示すために，が(4)を満足すると仮定する．すると，

が成り立つ．は次数 の多項式で，は より低い次数の非零の多項式なので，は で割り切れるが，ある については は割り切れないような の根 がある．がゼロならば， は で割り切れるだろうが，これは が で割り切れるということを意味するので，ありえない．従って，となる．性質 4は であるすべての多項式について であることを示している． はで生成されるイデアルのグレブナー基底なので，

となり，これでQE法の正確性が証明される．

以下で， から量限定子を除去する．ここで ，，である． は非零の定数なので，(2)はFalseとなり，等価のquantifier-freeの系は(4)で与えられる．また， は非零の定数なので，(4)はとなる：

任意の複素多項式系

FindInstance

FindInstanceでは任意の複素多項式系を扱うことができ，複素数解の例，あるいは空リスト（解のない系の場合）を与える．複数の例が要求された場合，例はReduceによって与えられた系のすべての解からランダムに生成される．1つの例が要求された場合は，1つの例だけを生成する，より高速なアルゴリズムが使われる．以下に挙げるのは，1つの例だけを見付ける，あるいは系に解がないことを証明するアルゴリズムである．

系に全称記号()が含まれる場合，QEアルゴリズムを使って，系が存在記号()だけを含むようになるまで，あるいは系がquantifier-freeになるまで，最内部の量限定子を削除していく．

は，に解があるとき，かつ，そのときに限り解を持つ．また，の解がであるならば，(1)の解はである．つまり，存在記号だけを含む系で解の例を見付けるためには，quantifier-freeの系の例が見付かるだけで十分なのである．さらに， のときにがのいずれかの解であるとき，かつ，そのときに限り，は

の解となるので，

の解の例を見付ける方法を示すことで十分なのである．まず，MonomialOrder->EliminationOrderという設定で に依存する多項式を除去し，のGroebnerBasis を計算する（不等式条件がない場合は， はMonomialOrder->DegreeReverseLexicographicと設定したのGroebnerBasisである）．もし に1が含まれる場合，解はない．含まれない場合は，次数逆辞書式順序の によって生成されたイデアルを法とする非常に独立な部分集合の中で，最大基数のの部分集合 を計算する（[1]のセクション9.3を参照のこと）．となるようにを並べ替え， で生成されたイデアルの辞書式順序GroebnerBasis を計算する．Wolfram言語では を計算するために，グレブナーウォーク法が使われる．

のときそれぞれの変数 について， には依存するがには依存しない の元の中で，最小の先頭単項式を持つ多項式 を選ぶ． の主係数を の多項式 とする． が にない変数に依存するならば， と で生成されたイデアルの辞書式順序グレブナー基底を に代入する．以下は，この操作により， が で生成されるイデアルを法として強く独立であるよう維持されることを示す．従って， を有限（多項式環のネーター性による）回拡大した後， の主係数 が ですべてにのみ依存するようになることがある．多項式集合 について， の要素の共通零点集合を とする．と の両方とも次元が で，であるため，の 次元の既約成分は の成分でもある． は のどの既約成分上でもゼロにならないので，の 次元既約成分上でもゼロにならない．よって， と のグレブナー基底には，にのみ依存する多項式 が含まれる． が成り立つとしよう．(2)の解を求めるために，となるような最後の 個の座標を選ぶ． ではすべて，なので，性質 4により，のとき が の最初の根に選ばれるなら，である．さらに となる．そうでないと，はに属すことになり，を意味する．しかしこのようなことは， が で割り切れるため，ありえないのである．

前述のアルゴリズムの正確さを証明するためには， にない変数に依存する で を拡大すると， で生成されるイデアルを法とした の強い独立性が維持されることを示さなければならない．任意の で， が にない変数に依存すると仮定する．が で生成されたイデアルを表し，が と で生成されたイデアルを表すとする．このとき にはの非零要素は含まれない．これを証明するために，で のときに であるとする．ここで のとき が成り立ち，

は で生成されたイデアルに属し， も同様である．これは の選択に反する．というのは， の頭単項式は に依存しており， の頭単項式よりも厳密に小さいからである．従って，の 上への投影は で密である．また，の次元は なので， は， への投影が で密であるような の任意の既約成分 上でゼロでなければならない．は 次元集合 の投影のZariski閉包なので，は の既約成分 の投影のZariski閉包に含まれる． は 次元なので， は 上でゼロであり， の への投影は で密である．これにより， が と で生成されたイデアルを法として強く独立であることが証明される．

以下は， を拡大する必要がある例である．ここでは ，，，である．は の2つの一次元成分のうちのどちらかでゼロである：

を で拡大すると，すべての強い独立性を維持しながら， だけに依存（実際は定数も）する となる：

Reduce

Reduceでは，任意の複素多項式系を解くことができる．第一段階として，ReduceはQEアルゴリズムを使って量限定子を除去する．得られたquantifier-freeの系が選言であるならば，選言の各項は別々に解かれ，解は項の解の選言として与えられる．従って，問題は以下の形式

のquantifier-freeの系を解くことに簡約される．まず，変数次数，MonomialOrder->LexicographicでのGroebnerBasis を計算し， に依存しない多項式を選ぶ．すると，の解集合は(3)の解集合と等しく， は の零点集合 のどの成分上でも消失しない． に1が含まれるならば(3)には解はない．それ以外の場合は， のときに には依存するが には依存しない の要素の集合 が，空にはならないような各 について， の最低の正の次元を持つ の要素 を選ぶ． の主係数 のうちの1つが 上でゼロ，つまり， で生成されるイデアルの基底に属すなら， を， と で生成されるイデアルの辞書式順序グレブナー基底で置換する．ここで，系を

の2つに分割し，選言(4)の最後の項以外のすべてについて再帰的に解法を呼び出す．代数集合 は厳密に に含まれているので，再帰は有限である． と すべての積が で生成されるイデアルの基底に属すならば，最後の項には解がない．そうでない場合は，性質 4により，最終項の解集合は

と等しくなる．条件 は，Roots[h_ij0,x_ij]で与えられる解（基底あるいはRootオブジェクトとして表される）すべてが正しく定義されていることを保証する．Reduceは返される不等式条件を簡約するために，複数の因数の削除，前の不等式条件と共通の因数の削除，モジュロ の還元，上で非零の因数の削除等，いくつかの操作を実行する．

オプション

Reduce，Resolve，FindInstanceのオプション

複素多項式系を解くためのWolfram言語関数には，操作方法を制御するオプションが数多く備わっている．このセクションでは，そのようなオプションを要約する．

複素多項式系の動作に影響を与えるReduce，Resolveのオプション

複素多項式系の動作に影響を与えるReduce，Resolve，FindInstanceのオプション

Backsubstitution

CubicsとQuartics

WorkingPrecision

ReduceOptionsグループのシステムオプション

ここで挙げるのは，複素多項式系でのReduce，Resolve，FindInstanceの動作に影響を及ぼすReduceOptionsグループのシステムオプションである．これらのオプションは以下のように設定する．

SetSystemOptions["ReduceOptions"->{"option name"->value}].

複素多項式系でのReduce，Resolve，FindInstanceの動作に影響を及ぼすReduceOptionsグループのオプション

AlgebraicNumberOutput

零次元イデアル を生成する方程式制約を持つ系では，Wolfram言語はグレブナー基底法を使って投影多項式を見付けるCAD法の変形を使う． のグレブナー基底の辞書式順序で，サイトの変数以外のすべての変数に線形多項式が含まれているなら，解の座標はすべて1つの代数的数の多項式，つまり最後の座標である．AlgebraicNumberOutputの設定は，Reduceが解座標を，最後の座標によって生成された場のAlgebraicNumberオブジェクトとして表すかどうかを決定する．

FinitePrecisionGB

Reduceでデフォルトで，GroebnerBasisをCoefficientDomain->Automaticの設定で使う．つまり，WorkingPrecisionを有限数 に設定しても，入力が厳密であるならGroebnerBasisでは厳密な計算が使われるということである：

ReorderVariables

デフォルトでは，Solveは指定された変数の順序を変えることができる．この例では，最初に について解いてから の解で を表した方が簡単である：

UseNestedRoots

参考文献