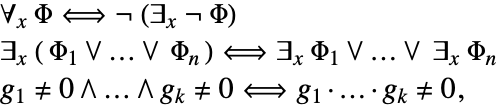介绍

Wolfram 语言中的函数 Reduce、Resolve 及 FindInstance 可以解决以方程或不等式表示的很多种问题. 这些函数使用一组算法来解决具有某些特殊性质的各类问题，或者使用试探法尝试将所给问题约化成一系列能用这些算法解决的问题. 本节教程将介绍用于解决关于复数多项式系统这类问题的算法，并对返回答案的结构以及影响所涉及方法各个方面的选项加以描述.

一个复数多项式系统是由多项式等式（方程）或不等式

结合使用逻辑运算符和量词

变量 在 或者 内部的出现，称为约束出现，任何其它情况下 的出现都称为自由出现. 如果复数多项式系统含有变量 的自由出现，则 被称作该系统的自由变量. 如果一个复数多项式系统不含量词，则该系统为无量词系统.

这个例子中的复数多项式系统含有自由变量 、 和 .

在 Wolfram 语言中，量词用函数 Exists () 和 ForAll () 表示.

任何复数多项式系统都可变换成前束范式

其中 是量词 或 ， 而 是无量词的.

任何无量词复数多项式系统都可变换成析取范式

其中 是多项式方程或不等式.

Reduce、 Resolve 以及 FindInstance 总是把复数多项式系统化为前束范式，无量词部分化为析取范式，并将等式或不等式的两边相减，化成这种形式

在复数多项式求解的所有教程中，假设系统已被转换成上述形式.

Reduce 可以求解任意复数多项式系统. 所得到的解 (可能已将 关于 扩展) 是下述形式中各项的析取:

其中 是系统中的自由变量， 为多项式， 是用根或 Root 对象表示的代数函数，并且合取式 (2) 中的任何一项都可缺少. 每一个 都是完全定义了的，即，对于任何满足合取式 (2) 中前面各项的 ， 中的分母或 Root 对象的首项不能为0.

Resolve 可以消除任意复数多项式中的量词. 如果不指明变量，结果将是这些项的逻辑组合：

其中 和 是多项式，每个 是系统的一个自由变量. 如果在输入时指明变量，Resolve 将给出与 Reduce 相同的答案.

FindInstance 可以处理任意复数多项式系统，给出复数解的实例或者，在无解情况下给出一个空列表. 如果要求的实例数大于1，这些实例将从系统的全部解集中随机生成，因此可能将取决于选项 RandomSeed 的值. 如果只需一个实例，将使用一种更快的只产生一个实例的算法，并且返回的实例永远相同.

求解复数多项式系统的主要工具是 Gröbner 基底算法 [1]，在 Wolfram 语言中作为 GroebnerBasis 函数使用.

Gröbner 基

理论

这一节将对 Gröbner 基理论作一个非常简短的介绍，仅讨论 Wolfram 语言求解复数多项式系统时所用算法的必要性质. 如果想要得到更详尽的介绍，请参见 [1, 2]等. 注意 [2] 中所说的单项式，在 [1] 称为项，反之亦然. 本节教程使用 [1] 中的术语.

的一个单项式是形如 的一个表达式，其中 为非负整数.

设 为 的所有单项式的集合. 一个单项式序是 上的一个线性序 ，使得对于所有的 ， ，且对于所有的 ，如果 ，则 .

令 为一个域、整数环或者在某一域上的一元多项式环. 令 和 为下面所定义的函数 . 若 是一个域，则 ，且 . 若 是整数环，则 和 为整数商和余数函数，其中. 若 某一域上的一元多项式环，则 和 为多项式的商和余数函数.

乘积 ，其中 为 上的非零元素， 是一个单项式，称之为项.

令 为 上的一个单项式序，并令 . 的首单项式 是 中出现的 -最大的单项式， 中的首项系数 是 中 的系数，而 中的首项 是乘积 .

在 中，相对于单项式序 的一个理想 的 Gröbner 基是多项式的一个有限集 ，其中对于每一个 ，存在 使得 被 整除. 每一个理想 都有一个 Gröbner 基 (证明参见 [1]).

令 ，并令 为一个单项式. 如果 能被 整除，且 ，则项 是模 可约的. 如果 模 可约， 那么 模 的约化是多项式

注意如果 ，则 ；否则 .

令 ，并令 为 的有序有限子集. 如果 包含一个模 的一个元素可约的项，则 是模 可约的. 模 的约化 由下述过程定义. 为 中模 的一个元素可约的项的集合，当此集合非空时，取 -最大单项式的项 ，取第一个 ，使得 模 可约，然后用 取代 中的项 . 注意后继步骤中所选的项 的单项式形成一个 -降序链，并且每个单项式能最多出现 次，其中 是 中元素的个数，然后程序终止.

如果对于所有 ， 模 不可约，并且如果 是整数环， ，则 Gröbner 基 为半约化.

Wolfram 语言中的函数 GroebnerBasis 返回半约化的 Gröbner 基. 下面的讨论中，假定所有的 Gröbner 基为半约化的. 注意这与文献中所定义的约化 Gröbner 基不同，因为这里基底多项式不必为首一多项式. 对于一个固定的单项式序，每一个理想都有一个唯一的的约化 Gröbner 基. 而这里定义的半约化 Gröbner 基可以相差一个 的可逆元素因子 (参见性质2).

性质1：令 为 中理想 的 Gröbner 基，并令 ，则当且仅当 时， .

这是根据定义得到的一个简单推论.

性质2：令 和 为相对同一单项式序 理想 的两个 Gröbner 基，并假设 和 中的元素按首多项式排序. 则有 并且对于 ，如果 为整数环，有 ；否则有 ，其中 为 中某可逆元素.

证明: 如果 ，则 模 可约，或者 模 可约. 因此，Gröbner 基中的元素的首单项式互不相同. 不失一般性，假设 . 为了归纳，固定 ，并假设对于所有的 ，对于 中某个可逆元素 ， . 若 为整数环，则 . 不失一般性，假设 . 由于 属于 ，因此存在一个 使得 整除 . 那么 ，所以 . 若 ，则 模 可约，也模 可约，由于 为半约化，这是不可能的. 因此 ，且 ， 能被 整除. 类似地， 能被 整除. 因此，在 中存在一个可逆元素 ，使得 . 如果 为整数环，则 和 均为正，因此 . 令 . 假设 . 由于 属于 ，存在 使得 一定能被 整除. 令 和 为 和 中在 的系数. 若 为一个域，则 中的项 模 可约，这与 为半约化的假设相矛盾. 若 为某一域上的一元多项式环，

因此， 模 可约，或者 模 可约，这与 和 为半约化的假设相矛盾. 最后，令 为整数环. 由于 不是模 可约， 也不是模 可约，因此有 和 . 因此 ，这是不可能的，因为 能被 整除. 因此得到 ，进而 . 对 进行归纳，即对于所有的 ，有 . 若 ，则对于 ，则 模某一个 可约，也即 按模 可约. 因此 ，性质2证毕.

性质3：令 为 上的理想，令 ，并令 为 上理想 的Gröbner 基. 则对于 上的可逆元素 ，当且仅当 时， 属于 的根.

如果一个理想包含 中的可逆元素，GroebnerBasis 始终返回 .

证明: 首先注意到对于任意非负整数 ，

属于理想 . 因此，如果 属于 的根，则 1属于 . 由于 为 的 Gröbner基，它必须含有一个元素 ，其首系数能除尽1. 因此 为 的可逆元素. 由于 为半约化，且 能除尽任意项，. 现在假设对于 中的一个可逆元素，. 则有 1属于 ，因此

其中 属于 ， 属于 . 因此，通过比较 的幂的系数，得到下述模 的等式：，在 时的 ，以及 . 这样，对于 ，有 ，而且 模 . 因此， 属于 的根，性质3证明完毕.

下面的性质技术性更强，对于求解复数多项式系统非常重要.

性质4：令 为 上理想 的 Gröbner 基， 有使得含 的单项式大于不含 的单项式的单项式序，令 为 中具有 的最小正次数 的元素，令 为 中相对 的首系数，令 为 中独立于 的所有元素. 那么对于任意多项式 和任意点 ，若 ，同时对于 ，，并且 ，则有 .

证明: 考虑 被作为 的多项式 相除得到的伪余式 .

由于 和 属于 ， 亦属于 . 由性质1，通过 对 约化必定为0. 由于 相对 的次数小于 ， 不能被 中任意依赖于 的元素约化. 因此

所以 . 由于 ，(1) 意味着 ，性质4的证明完毕.

Wolfram 语言函数 GroebnerBasis

Wolfram 语言函数 GroebnerBasis 得到半约化的 Gröbner 基. 本节讨论用于求解复数多项式系统的GroebnerBasis 选项.

用于求解复数多项式系统的 GroebnerBasis 选项.

CoefficientDomain

该选项指定系数的环 . 使用缺省设置 Automatic 时，系数环为输入中的数字系数生成的域.

Integers	整数环
InexactNumbers[prec]	精确度为 prec 的不精确数
Polynomials[x]	的多项式环
RationalFunctions	变量不在赋给 GroebnerBasis 的变量列表中的有理函数域
Rationals	有理数域

可用于 CoefficientDomain 的设置.

注意系数环 还取决于 GroebnerBasis 中 Modulus 选项的设置. 当 Modulus->p 时，对于素数 ，系数环为 ，或者，若 CoefficientDomain->RationalFunctions，系数环为 上有理函数域.

Method

在默认设置 Method->Automatic 下， GroebnerBasis 通常使用各种 Buchberger 算法. 另一种可用算法是Gröbner walk，这种算法使用较简单的单项式序计算 Gröbner 基，然后将其变换成所要求的较复杂的单项式序. 这种算法往往比直接按所要求的序计算要快，尤其是在已经知道输入的多项式是简单序的 Gröbner 基的情况下. 通过设置Method->Automatic，GroebnerBasis 使用默认设置为 CoefficientDomain->Rationals 和 MonomialOrder->Lexicographic 的 Gröbner walk.

使用 Gröbner walk 算法变换 Gröbner 基.

MonomialOrder

该选项指定单项式序. 选项的值可以是已命名的单项阶之一或者是一个权矩阵. 下面的表给出了 的条件.

Lexicographic
DegreeLexicographic
DegreeReverseLexicographic

单项式序.

量词的消去需要需要一个序，相对于这个序，含量词变量的单项式大于不含量词变量的单项式. Lexicographic 序符合这个条件，但下述的 EliminationOrder 通常使得计算速度加快.

其中 代表总次数， 代表自由变量， 代表量词变量， 和 为单项式， 代表DegreeReverseLexicographic 序.

使用 EliminationOrder 序时要求指定消除变量的 GroebnerBasis 语法.

消除序下的 Gröbner 基.

缺省设置下，带有设置 MonomialOrder->EliminationOrder 的 GroebnerBasis 去除结果中含有 的多项式，只返回关于 的基多项式. 要得到所有的基多项式，必须要改变 GroebnerBasisOptions 组中的系统选项 EliminateFromGroebnerBasis 的值 . (Wolfram 语言在量词消除算法中对选项进行局域修改.) 选项的值可以变为

SetSystemOptions["GroebnerBasisOptions"->{"EliminateFromGroebnerBasis"->False}].

系统选项 EliminateFromGroebnerBasis.

这里从 中消除了 . 结果是一个多项式，其零点是这两个原始方程的解集在 平面上的投影的 Zariski 封闭域(Zariski closure)：

在 平面上的解集的投影的确切描述取决于全部基多项式(basis polynomial). 注意如果 或 为0，那么第二个基多项式不能为0：

Resolve 给出在 平面上的解集的投影的确切描述：

决策问题

决策问题是变量全部被存在性量化(existentially quantified)的系统，即一个形如

的系统，其中 代表 中的所有变量. 解决一个决策问题意味着决定其是否等价于 True 或 False，也就是说，判断多项式方程和不等式 的无量词系统是否有解.

给定恒等式

后，任何决策问题的求解都可以转化为形如

的有限个决策问题的求解.

根据希耳伯特零点定理（Hilbert's Nullstellensatz）和 Gröbner 基的性质3

有复数解，当且仅当

对任意单项式序都不等于 {1} 时.

这里表明 有复数解：

这里表明 无复数解：

Wolfram 语言在解决决策问题时，GroebnerBasis 计算所用的单项式序为MonomialOrder->EliminationOrder，其中 {z} 指定为消除除变量列表. 这个设置与单项式序相对应，其中包含 z 的单项式大于不包含 z 的单项式，并且不包含 z 的单项式序为次数反字典序（degree reverse lexicographic）. 如果不含不等式条件，就没有必要引入 z，此时 Wolfram 语言使用MonomialOrder->DegreeReverseLexicographic.

量词消去

对于任何复数多项式系统，都存在一个等价的无量词复数多项式系统. 这由 Chevalley 定理得到. 这个定理指出，一个拟代数可构造集（quasi-algebraically constructible set，多项式方程和不等式的无量词系统的解集）的投影也是一个拟代数可构造集[3]. 量词消去是指找到与已知复数多项式系统等价的无量词多项式系统的过程. 在 Wolfram 语言中，复数多项式系统的量词消去是通过 Resolve 完成的. 它也被 Reduce 和 FindInstance 用作求解或查找复数多项式解的实例时的第一步.

对于复数多项式系统，Wolfram 语言使用下述量词消去方法. 已知恒等式

从任何复数多项式系统中消去量词可以转化为从形如

的系统中有限个单一存在性量词（single existential quantifier）的消去. 为了从 (1) 中消去量词，Wolfram 语言首先以一个使包含 的单项式大于不包含 的单项式的单项式序来计算方程的 Gröbner 基，

所用的单项式序为 EliminationOrder，其中 指定为消去变量列表和所保留的所有基多项式.

如果 不含依赖于 的多项式，则与（1）等价的无量词系统可通过令 中所有元素为零获得，并且声明作为 的一个多项式， 中至少有一个系数不等于零. 否则令 为 中具有 的最小正次数 的元素，令 为 的关于 的首系数，并令 为 中所有独立于 的元素. 现在 (1) 可以被分裂为两个系统

和

的析取.

为了从（2） 中消去量词， 量词消去步骤被以递归方式调用. 由于由 生成的理想严格包含由 生成的理想，多项式环的 Noetherian 性质保证了递归的有限性.

如果 属于 生成的理想的根，也即当1属于

时，(3) 等价于 False. 否则令

为 除以作为 的多项式的 所得的伪余式. 则（3）等价于无量词系统

为表明通过（3）能得到（4 ），假设 满足（3）. 则 且存在 ，使得

由于 和 属于由 生成的理想，

且 . 因此

这表明

为表明通过（4） 能得到（3）， 假设 满足（4）. 则有

由于 为 次的多项式，且 为次数小于 的非零多项式，所以在 中存在一个根 ，使得对于某 ， 能整除 ，但不能整除 . 如果 为零，则有 能整除 ，这是不可能的，因为这意味着 能整除. 因此 . 性质4 表明，对于任意多项式 ，. 由于 为 生成的理想的 Gröbner 基，所以有

这就完成了量词消去算法的正确性的证明.

下面是从 中消去量词. 这里 ，，且 . 由于 为非零常数，所以（2）为 False ，等价无量词系统由（4）给出. 由于 为非零常数，（4）变为 ：

任意复数多项式系统

FindInstance

FindInstance 可以应对任意复数多项式系统，给出复数解的实例，或者对无解系统给出空列表. 如果需要的实例数目大于1，则实例从由 Reduce 给出的系统的全部解中随机产生. 如果需要一个实例，将使用一种较快的生成一个实例的算法. 这里将描述找到一个实例或者证明系统无解所用的算法.

如果系统包含普通性量词（），将使用量词消去算法来消去最内部的量词，直到系统只含有存在性量词（），或无量词. 注意，

当且仅当 有解时有解，而且如果 为 的解，则 为（1）的解. 因此，要找到只含存在性量词的系统的解的实例，能找到无量词系统的实例就足够了. 再者， 为

的解的前提是当且仅当 为 之一的一个解，这里 . 因此只要表明如何找出

的解的实例就足够了.

首先计算 在单项式序 MonomialOrder->EliminationOrder 下的 GroebnerBasis ，消除依赖于 的多项式（如果无不等式条件， 为 在单项式序 MonomialOrder->DegreeReverseLexicographic 下的 GroebnerBasis ）. 如果 中包含1，则无解. 否则，计算 中模一个 生成的理想强独立的子集中基数最高的子集 ，而这个 是基于次数反字典序的（[1], 9.3节）. 重新对 排序使得 ，并计算由 生成的理想的字典序的 GroebnerBasis . Wolfram 语言使用 Gröbner walk 算法来计算 .

对于每一个变量 , ，选择 中依赖于 但独立于 的元素中具有最小首单项式的多项式 . 令 为作为 的多项式的 的首系数. 如果 依赖于 之外的一个变量，将则用 和 生成的理想的字典序 Gröbner 基替换 . 下面将表明该运算使得 模 生成的理想强独立. 因此，有可能在 进行有限次（由多项式环的 Noetherian 性质）扩展后，对于所有 ， 的首系数 仅取决于 . 对于多项式 集合 ，令 为 的元素的共同零点的集合. 和 的维数均为 ，且 ，因此 的任何 -维的不可约分量（ irreducible component）也是 的一个分量. 由于 不会对 的任何不可约分量为零，它也不会对 的任意 -维为不可约分量为零. 因此， 和 的 Gröbner 基包含一个仅依赖于 的多项式 . 令. 为求出（2）的解，取其最后 个坐标 ，以使 . 对于所有的 ，，因此根据性质4，如果对于 ，选取 为 的第一个根，则有 . 并且 ，否则 将属于 ，这将导致 ，但由于 整除 ，这是不可能的.

要证明前述算法的正确性，必须要证明，通过依赖于一个不在 中的变量的 来扩展 能保持 模 生成的理想的强独立性. 假设对于某个 ， 取决于一个变量，该变量不在 中. 令 表示 生成的理想，令 表示 和 生成的理想. 则有 不含 中的非零元素. 为证明这一点，假设 ，其中， . 那么 ，由于 ，以及

所以 属于 生成的理想， 也属于 生成的理想. 这与 的选择相矛盾，因为 的首单项式依赖于 ，并且严格小于 的首单项式. 因此， 在 上的投影对 是密集的，所以，由于 的维数为， 对于在 上的投影对 密集的 的某不可约分量 为零. 由于 为 -维集合 的投影的 Zariski 封闭域， 被包含在 的不可约分量 的投影的Zariski 封闭域上. 的维数为 ，因此 在 上为零，并且 在 上的投影对 密集，这就证明了 模 和 生成的理想强独立.

这是一个 需要扩展的例子. 这里 ，， ，并且 . 在 的两个一维分量中的一个上为零：

通过 扩展 ，导致在保持 的强独立性的同时，所有的 只依赖于 （事实上对于常数也成立）：

Reduce

Reduce 可以求解任意复数多项式系统. 作为第一步，Reduce 使用量词消去算法来消除量词. 若得到的无量词系统是一个析取，则析取的每一个项都可单独解出，并且解以各项的解的析取的形式给出. 这样，问题被约化为求解形如

的无量词系统.

首先计算变量次序为 ，单项式序为 MonomialOrder->Lexicographic 的 的 GroebnerBasis ，并选取独立于 的多项式. 然后 的解集等于（3）的解集，并且 在 的零点集 的任何分量上非零. 如果 中包含 1, 则（3） 无解. 否则，对于使得 中依赖于 但独立于任何 （）的元素的集合 非空的每一个 ，选择 中一个具有 的最小正次数的一个元素 . 如果 的首系数 中的某一个在 上为零，也就是说，它属于 生成的理想的根，则将 用 和 生成的理想的字典序 Gröbner 基替代. 现在把系统拆分为

并且对于析取（4）中除最后一项外的所有项递归地调用解题步骤. 注意代数集合 被严格包含在 中，因此递归是有限的. 若所有的 和 的乘积属于 生成的理想的根，则最后一项无解. 否则，根据性质4, 最后一项的解集等于

条件 保证了由 Roots[h_ij0,x_ij] 给定的所有解（由根或 Root 对象表示）有确切的定义. Reduce 执行多种动作来简化所返回的不等式条件，如去除多重因式，去除与先前不等式条件相同的因式，模 约化，以及去除 中非零因式等.

选项

用于 Reduce、Resolve 和 FindInstance 的选项

在 Wolfram 语言中，对于求解复数多项式系统的函数，有一些选项来控制函数的运行方式. 本节对这些选项作一总结.

Reduce 和 Resolve 中影响复数多项式系统的选项.

Reduce、Resolve 和 FindInstance 中影响复数多项式系统的行为的选项.

Backsubstitution

三次方程和四次方程

WorkingPrecision

系统选项的 ReduceOptions 组

这里是 ReduceOptions 组中可能影响到复数多项式系统的 Reduce、Resolve 和 FindInstance 的行为的系统选项. 这些选项可用以下方式设置

SetSystemOptions["ReduceOptions"->{"option name"->value}].

影响复数多项式系统的 Reduce、Resolve 和 FindInstance 的行为的 ReduceOptions 组选项.

AlgebraicNumberOutput

对于具有生成零维理想 的等式约束的方程组，Wolfram 语言使用 CAD 算法的变体，利用 Gröbner 基的方法求投影多项式. 如果 的字典序 Gröbner 基含有的线性多项式除了最后一个变量外的所有变量都含有常系数（一般情况下如此），则解的所有坐标是一个代数数的多项式，即最后一个坐标. AlgebraicNumberOutput 的设置决定 Reduce 是否将解坐标表示为由最后的坐标生成的域中的 AlgebraicNumber 对象.

FinitePrecisionGB

缺省情况下，Reduce 使用设置为 CoefficientDomain->Automatic 的GroebnerBasis. 这意味着即使将 WorkingPrecision 设置为一个有限的数值 ，如果输入为精确的，GroebnerBasis 将使用精确的计算：

ReorderVariables

在缺省情况下，允许 Solve 对指定变量进行重新排序. 在本例中，先求解 ，然后将 用 的解表示，较为容易：

UseNestedRoots

参考文献