Coefficient

Coefficient[expr,form]

gives the coefficient of form in the polynomial expr.

Coefficient[expr,form,n]

gives the coefficient of form^n in expr.

Details and Options

  • Coefficient picks only terms that contain the particular form specified. 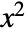is not considered part of .
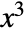  • form can be a product of powers.
  • Coefficient[expr,form,0] picks out terms that are not proportional to form.
  • Coefficient works whether or not expr is explicitly given in expanded form.

Examples

open allclose all

Basic Examples  (1)

Find coefficients of polynomials:

Scope  (4)

Find a coefficient at x:

Find a coefficient at a power of x:

Find the free term in a polynomial:

Find a coefficient at a multivariate monomial:

Options  (1)

Modulus  (1)

Find a coefficient over the integers modulo 2:

Properties & Relations  (2)

CoefficientList gives a list of all polynomial coefficients:

The same list of coefficients obtained using Coefficient and Exponent:

For multivariate polynomials CoefficientList gives a tensor of the coefficients:

CoefficientArrays gives the list of arrays of polynomial coefficients ordered by total degree:

The coefficient of x y3:

In cl the coefficient of x^a y^b is the element at position {a+1,b+1}:

In ca the position of this coefficient is a+b+1 followed by a 1s and b 2s (1 and 2 indicate the first and second variables):

Possible Issues  (1)

Coefficient treats transcendental powers as being algebraically unrelated to algebraic powers:

Coefficient treats distinct transcendental powers as being algebraically unrelated to one another:

Wolfram Research (1988), Coefficient, Wolfram Language function, https://reference.wolfram.com/language/ref/Coefficient.html (updated 1996).

Text

Wolfram Research (1988), Coefficient, Wolfram Language function, https://reference.wolfram.com/language/ref/Coefficient.html (updated 1996).

CMS

Wolfram Language. 1988. "Coefficient." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/Coefficient.html.

APA

Wolfram Language. (1988). Coefficient. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Coefficient.html

BibTeX

@misc{reference.wolfram_2024_coefficient, author="Wolfram Research", title="{Coefficient}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/Coefficient.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_coefficient, organization={Wolfram Research}, title={Coefficient}, year={1996}, url={https://reference.wolfram.com/language/ref/Coefficient.html}, note=[Accessed: 22-December-2024 ]}