Wolfram Mathematica Documentation Center
DOCUMENTATION CENTER SEARCH
New to Mathematica? Find your learning path »
Mathematica > Mathematics and Algorithms > Mathematical Functions > Special Functions > Elliptic Integrals > EllipticLog >
BUILT-IN MATHEMATICA SYMBOLTutorials »|See Also »|More About »

EllipticLog

EllipticLog
gives the generalized logarithm associated with the elliptic curve .
MORE INFORMATION
  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • EllipticLog is defined as the value of the integral 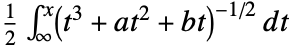, where the sign of the square root is specified by giving the value of y such that .
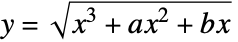  • EllipticLog can be evaluated to arbitrary numerical precision.
EXAMPLESCLOSE ALL
Basic Examples   (2)
Evaluate numerically:
Evaluate numerically:
In[1]:=
Click for copyable input
Out[1]=
In[2]:=
Click for copyable input
Out[2]=
 
In[1]:=
Click for copyable input
Out[1]=
Scope   (3)
Evaluate for complex arguments and parameters:
Evaluate to high precision:
The precision of the output tracks the precision of the input:
Applications   (1)
Define multiplication on the elliptic curve :
Use multiplication on the elliptic curve to add rational numbers:
Compare with EllipticLog:
Properties & Relations   (2)
Differentiation:
EllipticExp and EllipticLog are inverse functions of one another:
New in 1
Ask a question about this page  |  Suggest an improvement  |  Leave a message for the team
Format:   HTML  |  CDF