EllipticExp

EllipticExp[u,{a,b}]

is the inverse for EllipticLog. It produces a list {x,y} such that u==EllipticLog[{x,y},{a,b}].

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • EllipticExp gives the generalized exponential associated with the elliptic curve .
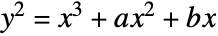  • For certain special arguments, EllipticExp automatically evaluates to exact values.
  • EllipticExp can be evaluated to arbitrary numerical precision.

Examples

open allclose all

Basic Examples  (2)

Evaluate numerically:

Check relation with the inverse function:

Plot the components of EllipticExp over several real periods:

Scope  (10)

Numerical Evaluation  (4)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number inputs:

Evaluate efficiently at high precision:

Specific Values  (3)

Values at fixed points:

Evaluate symbolically:

Value at zero:

Visualization  (2)

Plot the EllipticExp function for various parameters:

Plot the real part of EllipticExp[z,{1,2}]:

Plot the imaginary part of EllipticExp[z,{1,2}]:

Differentiation  (1)

First derivative with respect to u:

Plot the first derivative with respect to u when a=10 and b=1/3:

Applications  (4)

Define multiplication on the elliptic curve :

Use multiplication on the elliptic curve to add rational numbers:

Compare with EllipticLog:

Map integers on an elliptic curve:

Visualize the elliptic exponential in the complex plane:

Define multiplication on the elliptic curve :

Use multiplication on the elliptic curve to add rational numbers:

The value of EllipticLog at the product point equals the sum of values of EllipticLog at the corresponding factors:

Properties & Relations  (5)

Differentiation:

The point returned by EllipticExp[u,{a,b}] satisfies :

EllipticExp is closely related to the WeierstrassP function and its derivative:

Compare numerical values:

Evaluate the elliptic exponential and its derivative:

EllipticExpPrime can be expressed in terms of the components of EllipticExp:

WeierstrassHalfPeriods can be used to compute the two linearly independent periods of EllipticExp:

Compare numerical evaluations of EllipticExp at congruent points in the complex plane:

Possible Issues  (1)

EllipticExp is a doubly periodic complex function, so the inverse relation does not always hold:

The discrepancy equals two periods of the lattice:

Wolfram Research (1988), EllipticExp, Wolfram Language function, https://reference.wolfram.com/language/ref/EllipticExp.html.

Text

Wolfram Research (1988), EllipticExp, Wolfram Language function, https://reference.wolfram.com/language/ref/EllipticExp.html.

CMS

Wolfram Language. 1988. "EllipticExp." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/EllipticExp.html.

APA

Wolfram Language. (1988). EllipticExp. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EllipticExp.html

BibTeX

@misc{reference.wolfram_2025_ellipticexp, author="Wolfram Research", title="{EllipticExp}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/EllipticExp.html}", note=[Accessed: 05-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_ellipticexp, organization={Wolfram Research}, title={EllipticExp}, year={1988}, url={https://reference.wolfram.com/language/ref/EllipticExp.html}, note=[Accessed: 05-July-2025 ]}