DOCUMENTATION CENTER SEARCH
Mathematica
>
Special Functions
>
Built-in
Mathematica
Symbol
Special Functions
Tutorials »
|
LegendreP
SpheroidalQS
See Also »
|
Functions for Separable Coordinate Systems
Functions Used in Quantum Mechanics
Special Functions
More About »
LegendreQ
LegendreQ
[
n
,
z
]
gives the Legendre function of the second kind
.
LegendreQ
[
n
,
m
,
z
]
gives the associated Legendre function of the second kind
.
MORE INFORMATION
Mathematical function, suitable for both symbolic and numerical manipulation.
For integers
n
and
m
, explicit formulas are generated.
The Legendre functions satisfy the differential equation
.
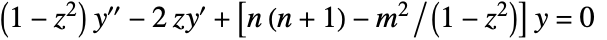LegendreQ
[
n
,
m
,
a
,
z
]
gives Legendre functions of type
a
. The default is type 1.
LegendreQ
of types 1, 2 and 3 are defined in terms of
LegendreP
of these types, and have the same branch cut structure.
For certain special arguments,
LegendreQ
automatically evaluates to exact values.
LegendreQ
can be evaluated to arbitrary numerical precision.
LegendreQ
automatically threads over lists.
EXAMPLES
CLOSE ALL
Basic Examples
(2)
Compute the 5
Legendre function of the second kind:
In[1]:=
Out[1]=
Plot:
In[1]:=
Out[1]=
Scope
(7)
Generalizations & Extensions
(3)
Applications
(2)
Properties & Relations
(1)
SEE ALSO
LegendreP
SpheroidalQS
TUTORIALS
Special Functions
MORE ABOUT
Functions for Separable Coordinate Systems
Functions Used in Quantum Mechanics
Special Functions
New in 1 | Last modified in 3
© 2008 Wolfram Research, Inc.
![(1-z^2)y^(′′)-2zy^′+[n(n+1)-m^2/(1-z^2)]y=0](Files/LegendreQ.en/3.gif "(1-z^2)y^(′′)-2zy^′+[n(n+1)-m^2/(1-z^2)]y=0"){kind=small}
.
EXAMPLES
Basic Examples 
Scope 