DOCUMENTATION CENTER SEARCH

Mathematica >

Built-in Mathematica Symbol

Tutorials »|See Also »|More About »

Rationalize

Rationalize[x]
converts an approximate number x to a nearby rational with small denominator.

Rationalize[x, dx]
yields the rational number with smallest denominator that lies within dx of x.

MORE INFORMATION

Rationalize[x, dx] works with exact numbers x.

Rationalize[x] yields x unchanged if there no rational number close enough to x to satisfy the condition 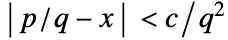p/q-x<c/q², with 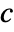c chosen to be 10^-4.

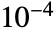Rationalize[x, 0] converts any x to rational form. »

Basic Examples (1)

Convert to a rational number:

Applications (3)

Properties & Relations (3)

N Chop Round ContinuedFraction Convergents RootApproximant LatticeReduce FindSequenceFunction

Numerical Functions

Continued Fractions & Rational Approximations

Number Recognition

Number Theory

Demonstrations with Rationalize (Wolfram Demonstrations Project)

New in 1 | Last modified in 4

Ask a question about this page | Suggest an improvement | Leave a message for the team