BUILT-IN MATHEMATICA SYMBOL

VectorAngle

gives the angle between the vectors u and v.

MORE INFORMATION

VectorAngle gives an angle in radians.

For nonzero real vectors the vector angle 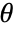satisfies .

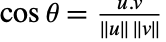For complex vectors the numerator is .

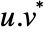EXAMPLES

CLOSE ALL

Basic Examples (2)

The angle between two vectors in 2D:

The angle between two vectors in 3D:

The angle between orthogonal vectors:

The angle between two vectors in 2D:

In[1]:=

Out[1]=

In[2]:=

Out[2]=

The angle between two vectors in 3D:

In[3]:=

Out[3]=

In[4]:=

Out[4]=

The angle between orthogonal vectors:

In[1]:=

Out[1]=

In[2]:=

Out[2]=

In[3]:=

Out[3]=

Scope (2)

Use exact arithmetic to compute the vector angle:

Use machine arithmetic:

Use 47-digit precision arithmetic:

Use symbolic vectors:

Generalizations & Extensions (1)

For complex vectors the angle returned may be complex:

Applications (3)

Find when two vectors have the same direction:

Find the area of the triangle with u and v as two sides:

Plot the area in the triangle formed by the

axis and a unit vector in the first quadrant:

Distribution of angles between random vectors with positive entries in 2, 3, 5, and 10 dimensions:

Properties & Relations (6)

The vector angle

satisfies

:

The generalization to complex vectors satisfies

:

If you rotate a vector u in a plane that includes u, then the vector angle is the rotation angle:

If you rotate it in a plane that does not include u, then the angles differ:

The vector angle

is related to the cross product through

:

ArcTan of two arguments gives the signed vector angle between the

axis and the vector:

Eigenvectors are the vectors for which the angle between

and

is 0:

Possible Issues (1)

The angle between the zero vector and any other vector is indeterminate: