zero of the Riemann zeta function on the critical line.
zero with imaginary part greater than 
ZetaZero
zero of the Riemann zeta function on the critical line.
zero with imaginary part greater than 
Details
- Mathematical function, suitable for both symbolic and numerical manipulation.
- For positive k, ZetaZero[k] represents the zero of
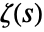on the critical line 
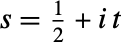that has the k
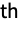smallest positive imaginary part. - For negative k, ZetaZero[k] represents zeros with progressively larger negative imaginary parts.
- N[ZetaZero[k]] gives a numerical approximation to the specified zero.
- ZetaZero can be evaluated to arbitrary numerical precision.
- ZetaZero automatically threads over lists.
Examples
open all close allBasic Examples (3)
Scope (8)
Numerical Evaluation (3)
Specific Values (3)
Visualization (2)
Generalizations & Extensions (1)
Negative order is interpreted as a reflected root of the Zeta function:
Applications (5)
Plot distances between successive zeros:
Compute Gram points:
Show good Gram points, where RiemannSiegelZ changes sign for consecutive points:
First occurrence of Lehmer's phenomenon:
Plot an approximation of the number of primes and prime powers using MangoldtLambda and ZetaZero:
Properties & Relations (1)
Possible Issues (1)
ZetaZero[0] is not defined:
Text
Wolfram Research (2007), ZetaZero, Wolfram Language function, https://reference.wolfram.com/language/ref/ZetaZero.html.
CMS
Wolfram Language. 2007. "ZetaZero." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ZetaZero.html.
APA
Wolfram Language. (2007). ZetaZero. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ZetaZero.html