Introduction to Constrained Optimization in the Wolfram Language
Optimization Problems
Constrained optimization problems are problems for which a function 
is to be minimized or maximized subject to constraints 
. Here 
is called the objective function and 
is a Boolean-valued formula. In the Wolfram Language the constraints 
can be an arbitrary Boolean combination of equations 
, weak inequalities 
, strict inequalities 
, and 
statements. The following notation will be used.
stands for "minimize 
subject to constraints 
", and
stands for "maximize 
subject to constraints 
".
You say a point 
satisfies the constraints 
if 
is true.
The following describes constrained optimization problems more precisely, restricting the discussion to minimization problems for brevity.
Global Optimization
A point 
is said to be a global minimum of 
subject to constraints 
if 
satisfies the constraints and for any point 
that satisfies the constraints, 
.
A value 
is said to be the global minimum value of 
subject to constraints 
if for any point 
that satisfies the constraints, 
.
The global minimum value 
exists for any 
and 
. The global minimum value 
is attained if there exists a point 
such that 
is true and 
. Such a point 
is necessarily a global minimum.
If 
is a continuous function and the set of points satisfying the constraints 
is compact (closed and bounded) and nonempty, then a global minimum exists. Otherwise a global minimum may or may not exist.
Local Optimization
A point 
is said to be a local minimum of 
subject to constraints 
if 
satisfies the constraints and, for some 
, if 
satisfies 
, then 
.
A local minimum may not be a global minimum. A global minimum is always a local minimum.
Solving Optimization Problems
The methods used to solve local and global optimization problems depend on specific problem types. Optimization problems can be categorized according to several criteria. Depending on the type of functions involved there are linear and nonlinear (polynomial, algebraic, transcendental, ...) optimization problems. If the constraints involve 
, you have integer and mixed integer-real optimization problems. Additionally, optimization algorithms can be divided into numeric and symbolic (exact) algorithms.
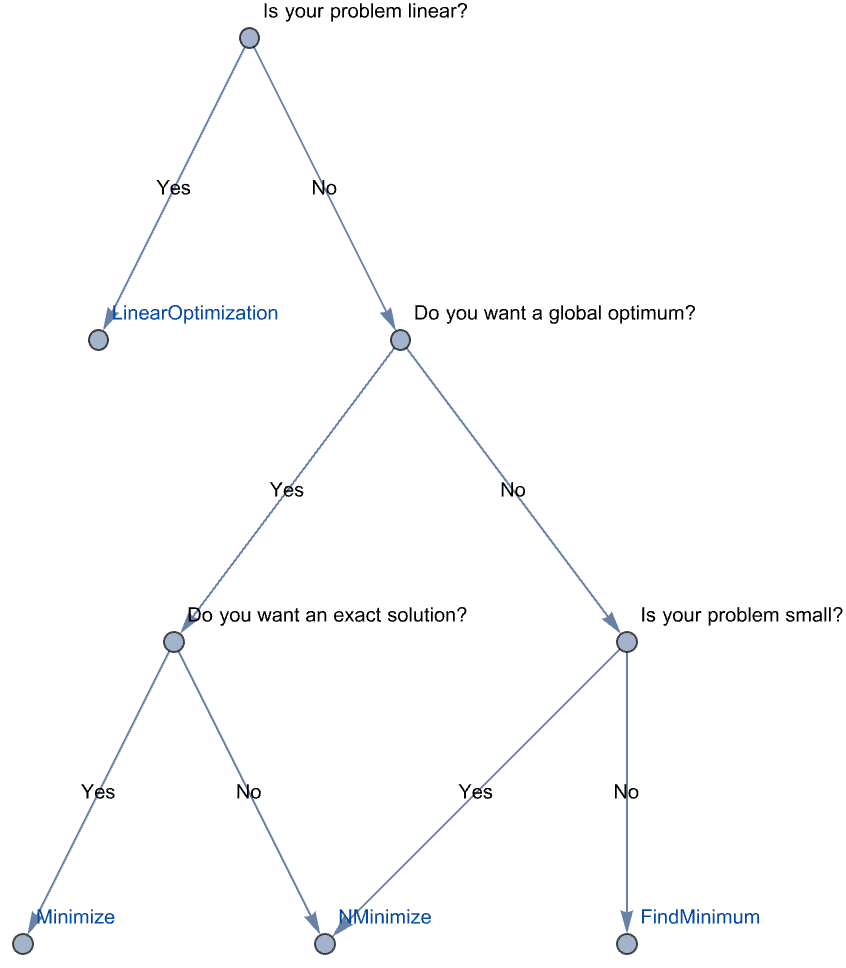
Wolfram Language functions for constrained optimization include Minimize, Maximize, NMinimize, and NMaximize for global constrained optimization, FindMinimum for local constrained optimization, and LinearOptimization for efficient and direct access to linear optimization methods. The following table briefly summarizes each of the functions.
Function | Solves | Algorithms |
| FindMinimum,FindMaximum | numeric local optimization | linear programming methods, nonlinear interior point algorithms, utilize second derivatives |
| NMinimize,NMaximize | numeric global optimization | linear programming methods, Nelder-Mead, differential evolution, simulated annealing, random search |
| Minimize,Maximize | exact global optimization | linear programming methods, cylindrical algebraic decomposition, Lagrange multipliers and other analytic methods, integer linear programming |
| LinearOptimization | linear optimization | linear optimization methods (simplex, revised simplex, interior point) |
Summary of constrained optimization functions.
Here is a decision tree to help in deciding which optimization function to use.
