デカップリングを使用したシミュレーションのトラブルシューティング
このチュートリアルに使用されているモデル
|
| SimpleStep StepSquared Feedback FilteredFeedback |
はじめに
方程式ブラウザを使うとモデルの数学面と物理面の両方が改善できる.また,シミュレーション動作を理解することができるようになり,パフォーマンスの障壁の可能性が排除される.さらに,モデルを適切に初期化する方法,つまり,モデルの変数の適切な初期値を選ぶ方法が理解できる.一般に方程式ブラウザはさまざまな経験レベルのユーザにサービスを提供する強力なツールである.
このドキュメントは方程式ブラウザの使い方を段階を追って説明するものである.また,問題を解く標準的な方法の一つである「デカップリング」とも呼ばれる「分割統治法」を使い始めてモデルをスピードアップする助けにもなっている.非常に簡単なモデルから始めてパフォーマンスを改善するモデリングのヒントを学んでいく.また,モデルの背後に潜む数学と物理についても簡単に説明する.このチュートリアルで説明しているモデルはいくつかのドラッグアンドドロップ操作で簡単に作成できる.DocumentationExamples.Tutorial.Decouplingでバンドルされているドキュメントの例を開いてみるのもよいだろう.
方程式ブラウザのより包括的なドキュメントはドキュメントセンターの対応セクションを参照されたい.ドキュメントセンターには,Model Center,Simulation Centerおよび方程式ブラウザのヘルプメニューからアクセスできる
簡単な例
System Modelerはシミュレーションを実行する前に与えられたモデルの方程式システムを異なるブロックに分類する.これらのブロックは,それぞれができるだけ少数の方程式を具体化するような方法で作られている.一つのブロックに入れられる方程式数の上限はないが,どの方程式ブロックにも少なくとも一つの方程式がなければならない.
自然言語から類推して,変数とパラメータは単語,方程式は文,ブロックは段落と考えることができるだろう.単語,文,段落の数が少なく簡単なテキストの方が,例えば人間の脳にとって理解と処理が簡単になるのは明らかである. 同じことがモデルおよび方程式ブロックにも言える.つまり,方程式のブロック数が少なく簡単な方が理解と改善が簡単なのでより望ましい.自然言語からの別の有益な類推に,テキスト中の段落の順番は勝手に変えられないというものがある.例として,段落が2つの単純なテキストについて考えてみよう.最初の段落にある概念を X と定義し,これを2番目の段落にある概念 Y の基盤とする.この2つの段落の順番を逆にすることは意味をなさない.X の説明なしで Y は導入できないからである.数学という言語では,これを Y は X に依存すると言う.同様に,モデル内の方程式を理解してそれを解き分析するためには方程式ブロックの順序が重要になる.方程式ブラウザはまずブロックと方程式の依存関係を推測し,それに従ってそれらを並べる(ソートする)のである.
明確にするために,ブロックは色スキームに従って色分けされている.こうすることで,ブロックを所属するカテゴリに基づいて見分けるのが簡単になる.方程式システムを分類する方法には,「システムクラス」,「変数の領域」,「時間変動制」の3つがある.また,この分類に関連づけられた3種類の異なる彩色法がある.このチュートリアルでは最初に挙げた分類方法,つまりシステムクラスに焦点を当てる.次の図はさまざまなシステムクラスの色スキームを簡単で簡潔な方法で説明している.
一般に,方程式ブロックは緑と青の側に留まるようにするといいだろう.可能であれば黄色や赤の側は避けるのが賢明だ.前者の方程式システムは線形方程式に対応する.後者の方程式システムは非線形および数値のJacobiansに対応し,誤った結果やパフォーマンスの障壁になる可能性を孕んでいるからである.
System Modelerは最初からさまざまな複雑さの幅広いモデルのシミュレーションや処理を行うことができる.しかし,モデルが思ったように動かないこともあるだろう.そのような場合には方程式ブラウザを参照するとよい.特に,最大の方程式システムと対応するシステムクラスを特定してそれがどうしてそれ以上小さい方程式システムに分割できないのかを調べてみるとよい.これは,モデルが非線形方程式と数値のJacobiansを含む数多くの大規模方程式システムを含んでいる場合には重要である.しばしば一つの方程式システムを簡約するだけで問題全体が修正されたりパフォーマンスが著しく向上したりするものである.
最初から
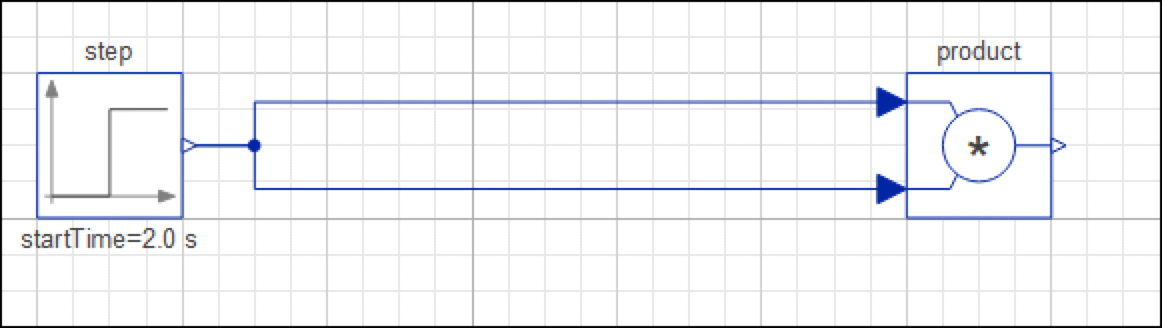
まず,最初の例を少しずつ構築してみよう.最初にソース成分であるStep成分を加える.名前が示すようにこの成分はtime = 0からt = startTimeとなるまで一定の出力信号 y = offsetを生成し,その後は y = height + offsetの一定の出力を生成する.成分のパラメータ値は以下のように設定する.このモデルは段取るされているドキュメントの例にSimpleStepという名で含まれている.
単一のStep成分を含むSimpleStepモデルのダイアグラムビュー
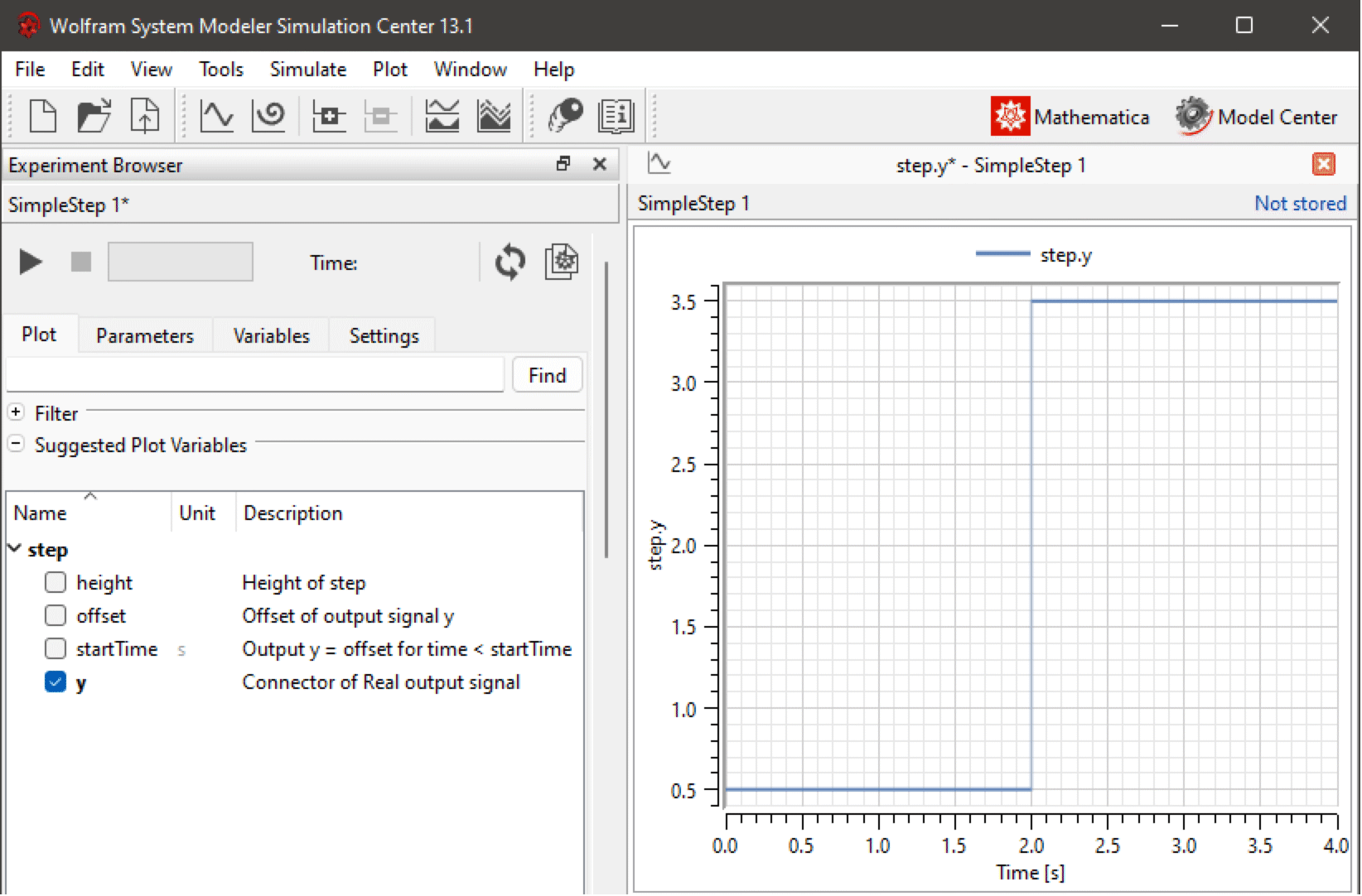
これはまだそれほど役立ちそうには見えないが,それでもシミュレーションが可能なスタンドアロンのモデルとして動作する.これを最初のブリックとしてそこに単純なモデルを組み立てる.次に実行ボタンをクリックして,あるいはCtrl+Shift+3を押してモデルのシミュレーションを行う.Simulation Centerが現れたらy変数を選択して以下のようにプロットする.
Simulation Centerで表示された時間の関数としての yのプロット
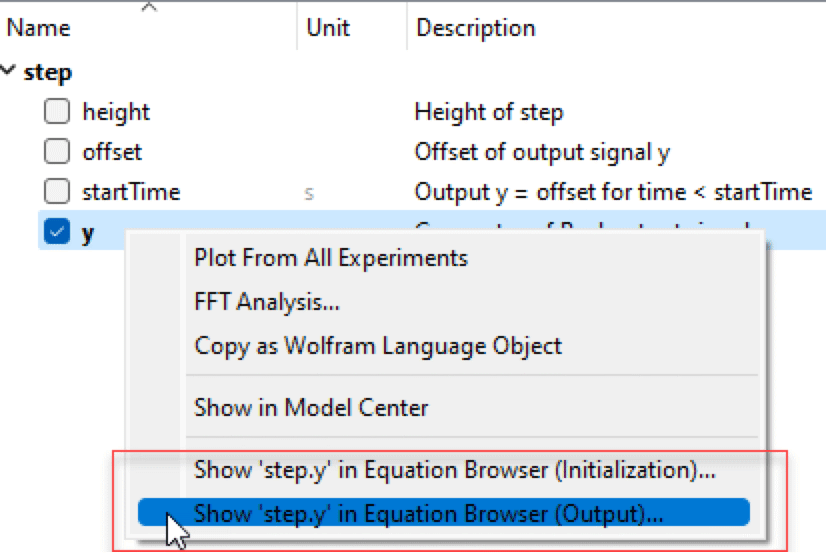
Step成分のパラメータに対して設定した初期値から予想されるように,yの値は2秒間は0.5で,その後は3.5に跳ね上がる.次に方程式ブラウザを開くのだが,これには2つの方法がある.Ctrl+3を押すか,あるいは yパラメータを右クリックして.以下のようなポップアップメニューで方程式ブラウザを指しているメニュー項目のいずれかを選べばいいのである.
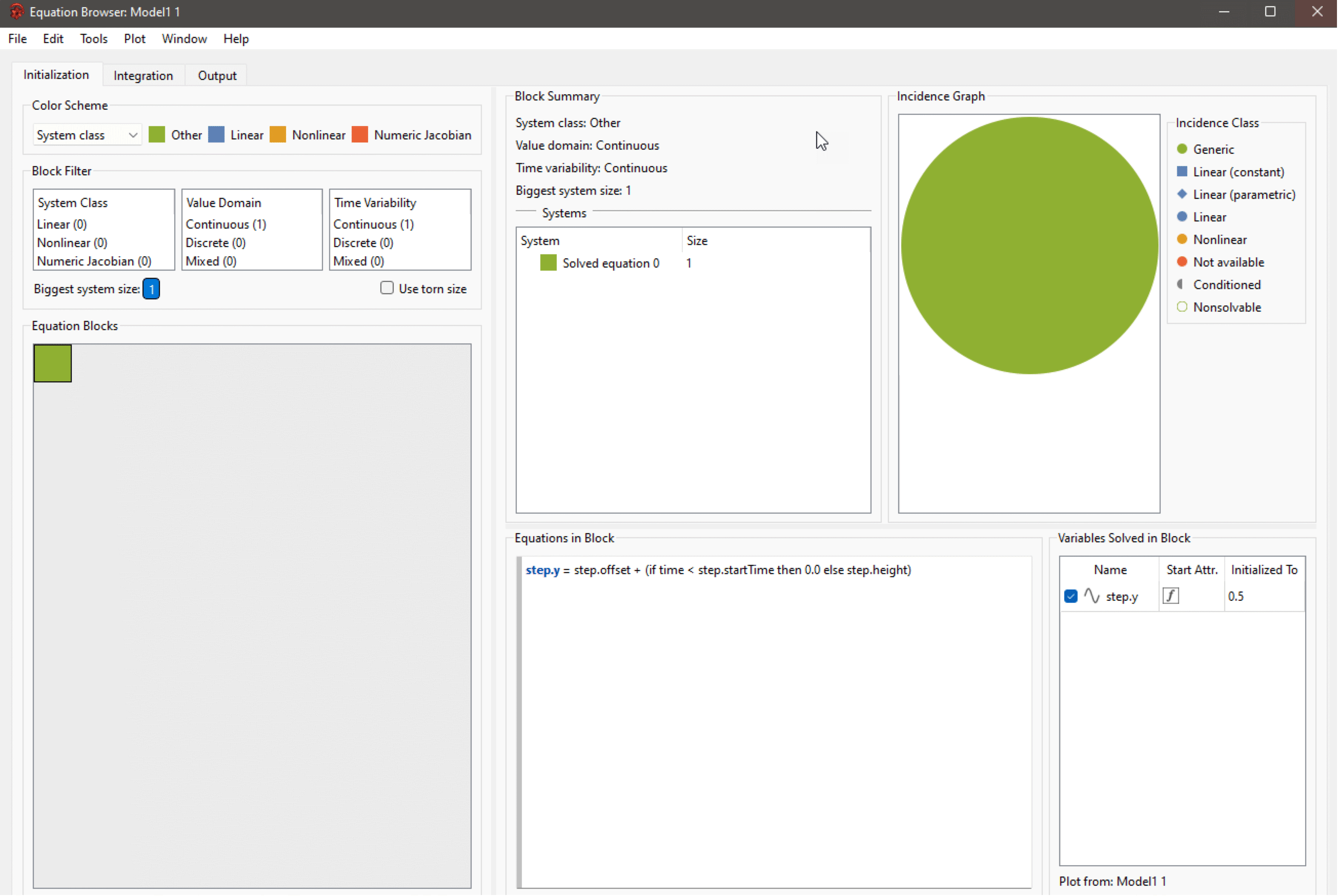
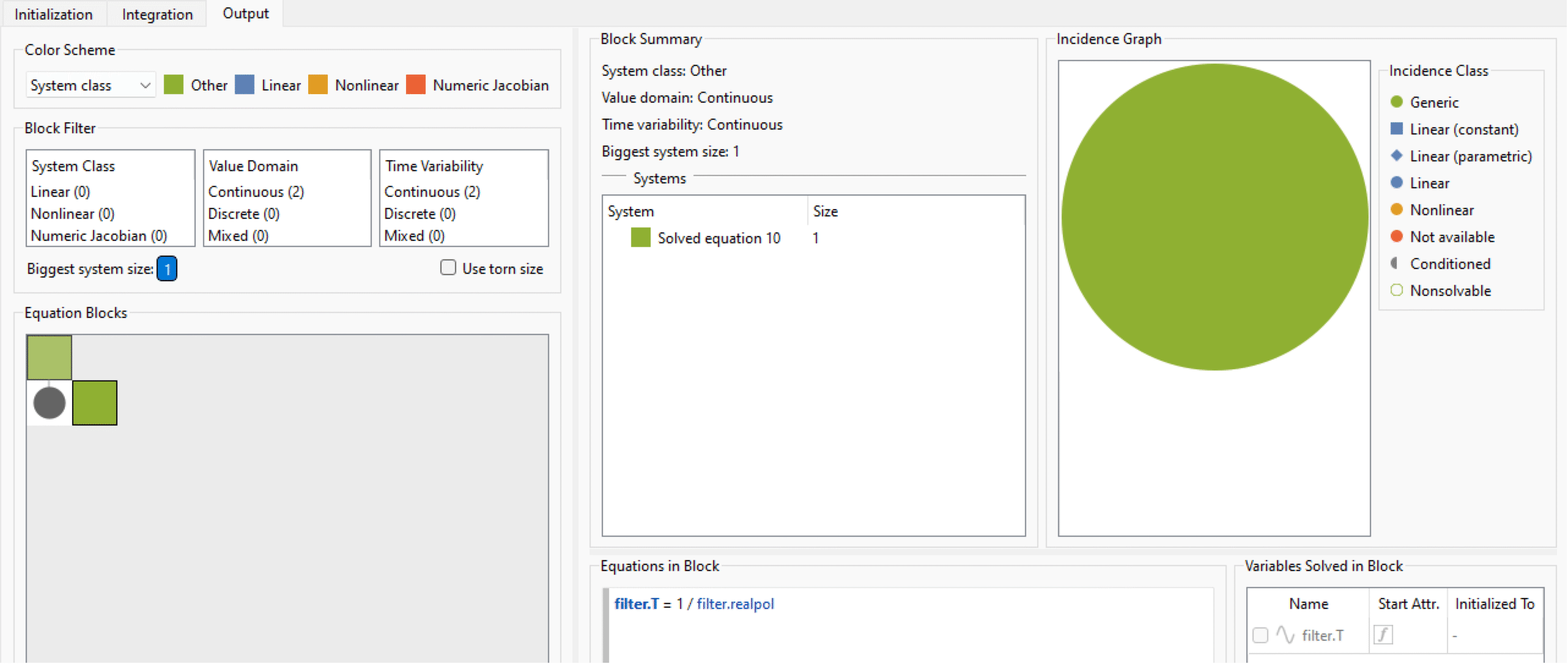
ポップアップメニューの(Outputで終っている)最後の項目をクリックするかキーボードショートカットを使うかすると,以下のように方程式ブラウザが開く.
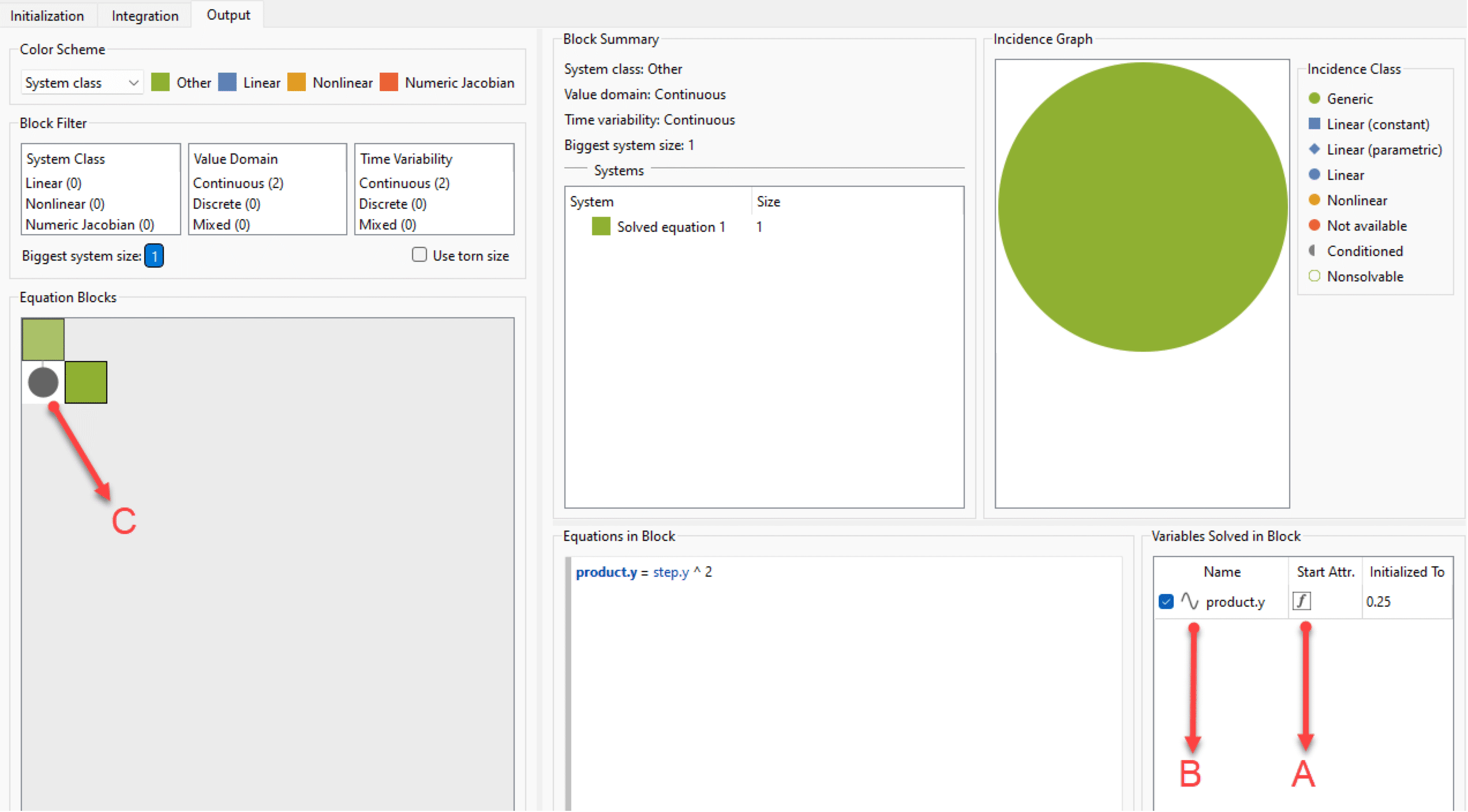
これで方程式ブラウザのOutputタブの状態になった.左下のパネルが示すように方程式ブロック一つしかない.このブロックは方程式システムを一つだけ含んでいて,そこに含まれる方程式も一つだけである(下中央のパネルを参照のこと).したがって,このシステムの大きさは最大のシステムの大きさでもあり,それは1である.唯一の方程式には簡単なIF文が含まれているので緑で表示されている.これは,何も複雑なこと(非線形や数値ヤコビアン)がないことを示している. これはよい知らせである.ここで言っておきたいのだが,すべてのブロックを緑や青にすること,非線形ブロックや数値ヤコビアンを完全に回避することは常に可能な訳ではないのである.多くのモデルにはそのような非線形方程式が意図的に含まれているものだ.しかし,可能であればそのようなシステムを回避するように試すべきだろう.
ブロック中の方程式を解くための変数は右下のパネルに表示される.この場合は最初に0.5に設定されたy (step.y)しかない.文字Aで指定されたアイコンと対応する赤い矢印のアイコンはyが関数または条件(この場合はIF文)によって初期化されたことを示している.言い換えるなら,これはSystem Modelerがそのような変数を初期化するために設定した値を無視(オーバーライド)することを示している.初期化問題に特化した別のチュートリアル(モデルの初期化のトラブルシューティング)でそのような動作の意味と利点について学ぶ.アイコンBアイコンはyが時間的に連続であることを示している.
次にProduct成分を加えて以下のようにこれをstepと接続する.StepSquaredの例を見るのもよいだろう.
Step成分とProduct成分を含むStepSquaredモデルのダイアグラムビュー
このモデルのシミュレーションを行い,方程式ブラウザブラウザを開く.図からも分かるように,2つのブロックが対角上に並んでいる.最初のブロック(左上隅)は前のステップと同じままである.2番目のブロックには入力を単純に二乗する方程式が一つ含まれている.アイコンCは最初のブロック(step.y)の出力/結果が第2ブロックで使われたあるいはこれにフィードされたことを示している.興味深いことにSystem Modelerはproduct成分の両方の入力が同じソースからのもので等しく,したがって方程式には掛け算ではなく指数(step.y^2)が含まれていることを自動的にピックアップしている.素晴らしい!
Step成分とProduct成分を含むモデルの方程式ブロック
潜在的な障壁の識別
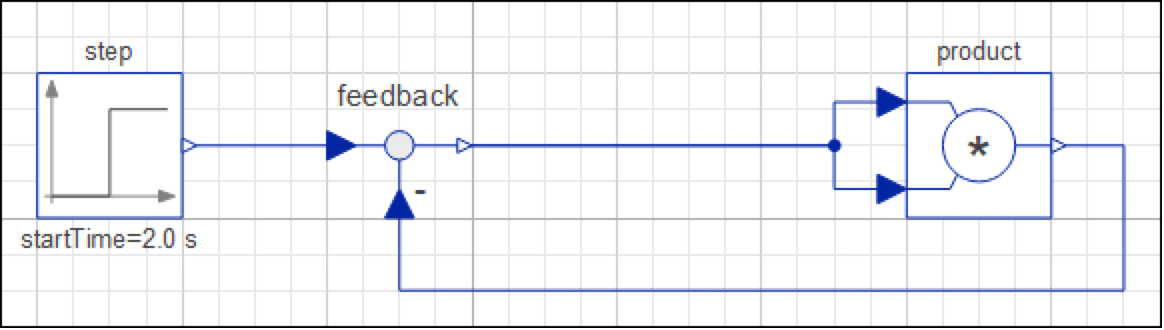
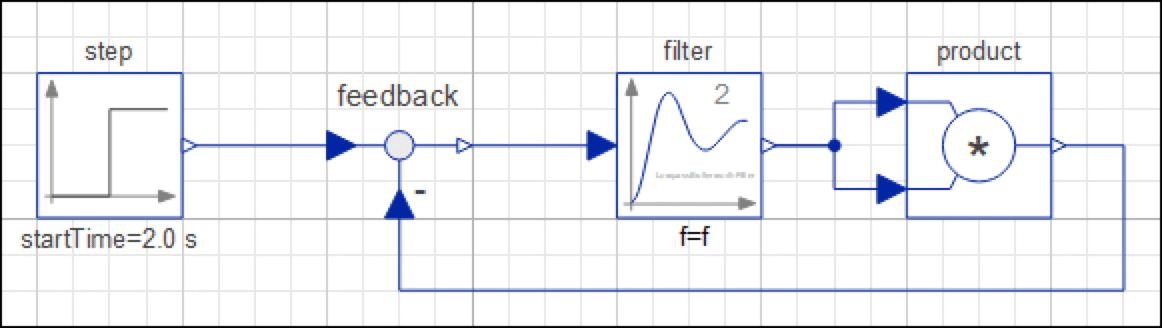
次に,Feedback成分というもう1レベル上の複雑さを加えよう.モデルの図は次のようになる.
Feedback モデルのダイアグラムビュー
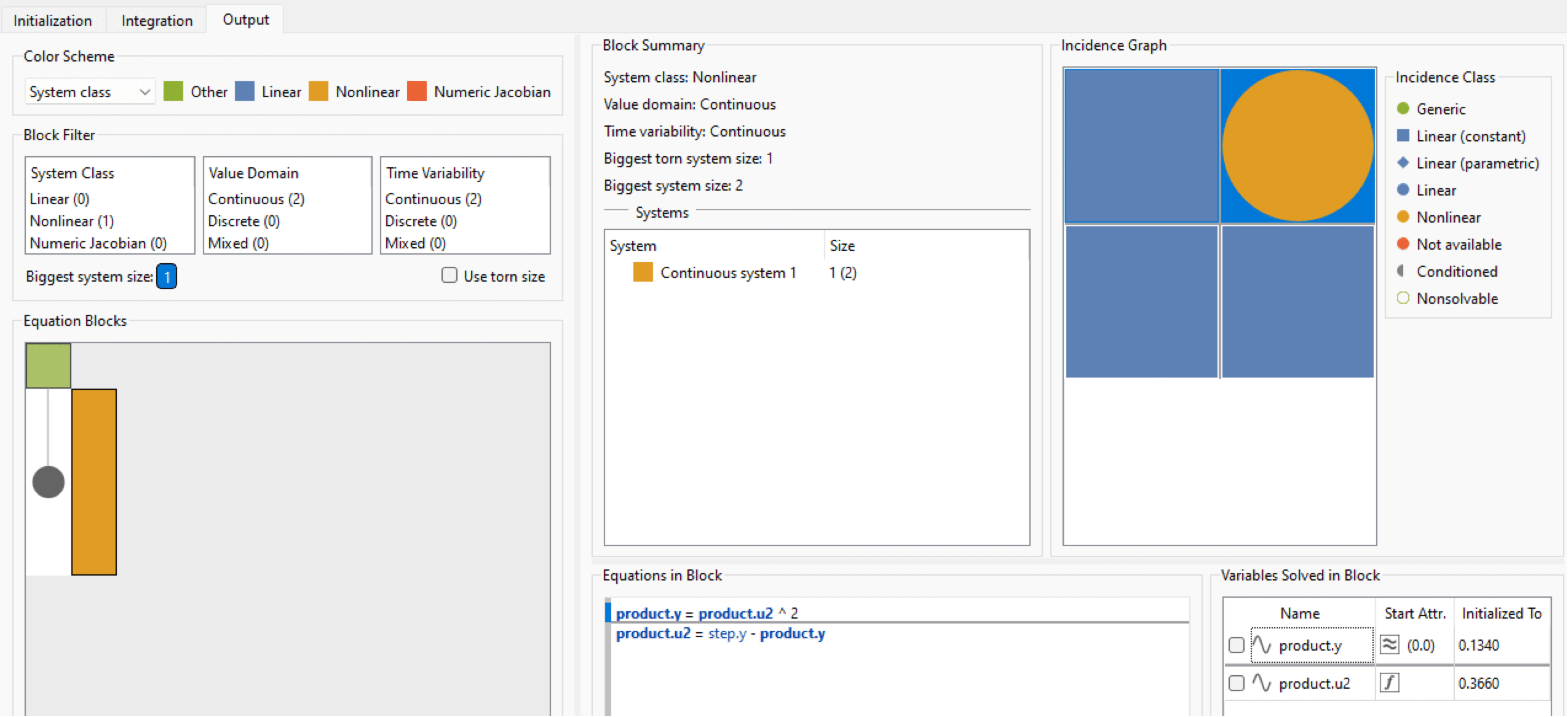
Feedbackモデルのシミュレーションを行って方程式ブラウザを調べると,非線形方程式システムがオンレンジ色で表示されている.先に述べた通り,これは望ましいことではなく,可能であればこのようなシステムは回避したい.
非線形方程式システムに加え,(右上パネルの)Incidence Graphが前のステップのように単純な緑の円で構成されているのではなく22行列になっている.Incidence Graphは各方程式の変数間の関係をいわゆる「出現クラス」を使って分かりやすく説明する.
Incidence Graphは方程式システムをさらに詳しくあるいは豊かに表現したものと考えることができる.グラフの各行は一つ方程式に対応する.オレンジ色のブロックには2つの方程式があるのでIncidence Graphの行は2つになる.グラフの列は方程式の変数を表す.色スキームは出現クラスを決定する.ご想像の通り,スペクトルの緑の側が望ましい.オレンジ色の円をクリックするかこの上にカーソルを持ってくるかすると,この非線形性がproduct.u2によるものであることが分かる.これはfeedback成分の結果として出現したものであるが,これはproduct (product.u2)成分の入力がその出力(product.y)に依存するようにしていて,入力と出力の間にループ(円環)する依存関係を生んでいる.
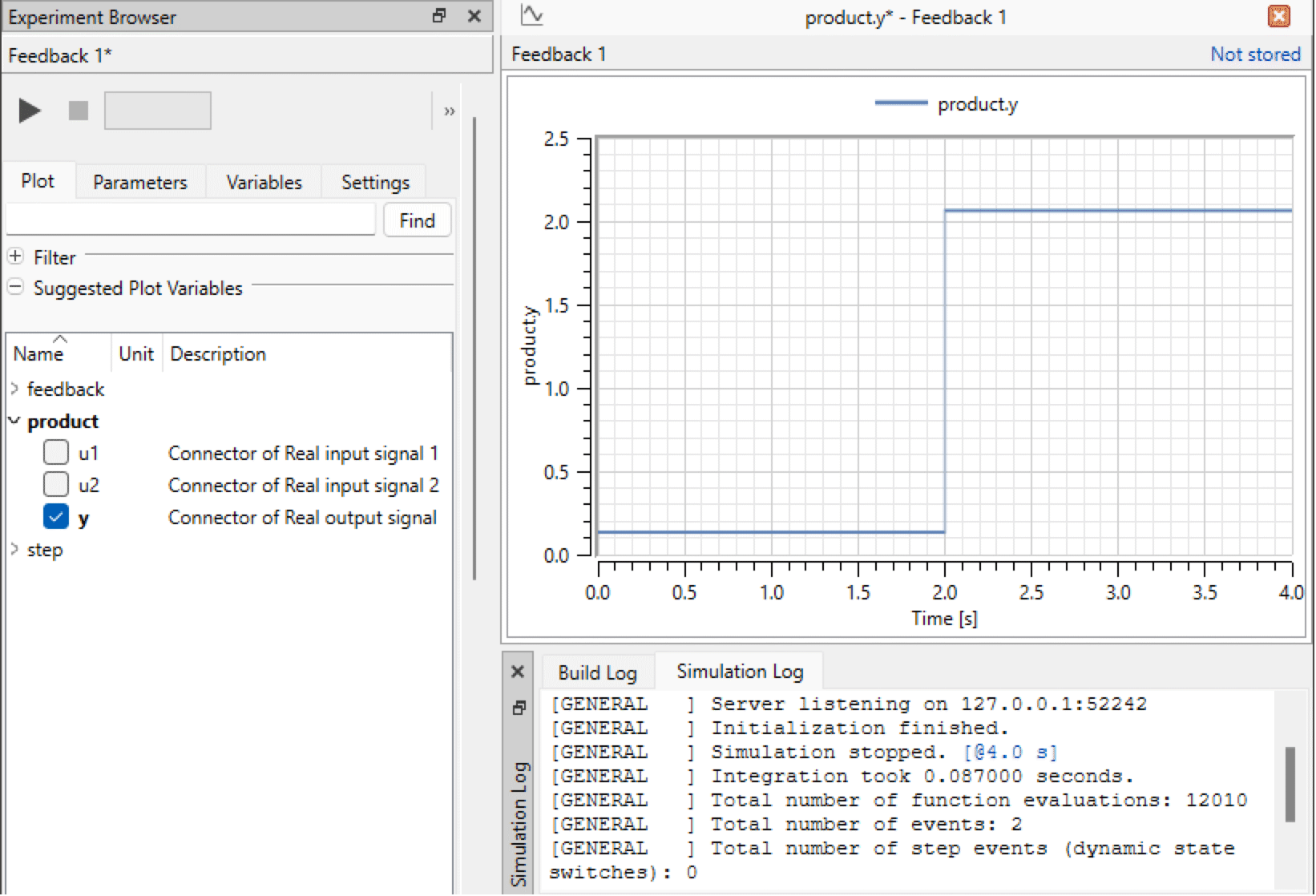
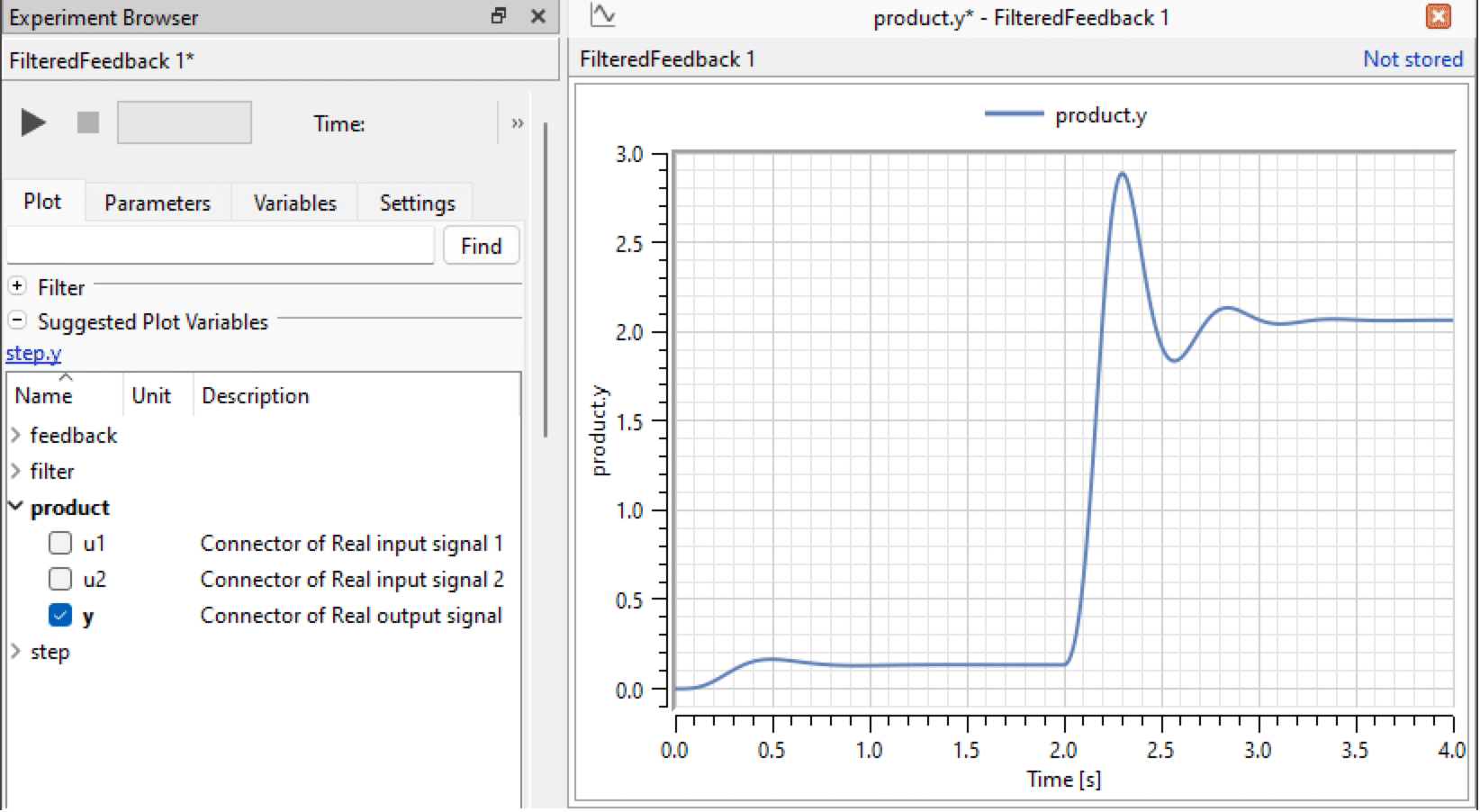
以下のようにproductの出力をプロットするのもいいだろう.フィードバックループにはダイナミクスがなく,したがって,示されているように出力がstep.yの静的関数である点に注意されたい.
Simulation Centerに表示されたシミュレーションログ
ローパスフィルタを加える
前述の非線形方程式システムの存在は入力の出力に対する循環的依存性によるものであり,逆もまた同様であることが分かった.このループを断ち切って出力から入力を切り離すことができれば,この問題に対処できるだろう.明らかに,解決は一意的なものではなく,product成分の入出力を切り離す方法はいろいろあるだろう.例えば,LowpassButterworthのようなフィルタをfeedbackとproductの間に加えることでもこれは達成できる.試してみよう.フィルタ成分のパラメータをデフォルト値に保ってFilteredFeedbackモデルのシミュレーションを行おう.
filter成分を加えたFilteredFeedbackモデルのダイアグラムビュー
方程式ブラウザを見ると分かるように,非線形方程式システムが奇跡のように消失して,また緑のブロックに戻ったではないか!
これは,フィルタがループを切断してシステムを分離したためである.つまり分割統治したわけだ.
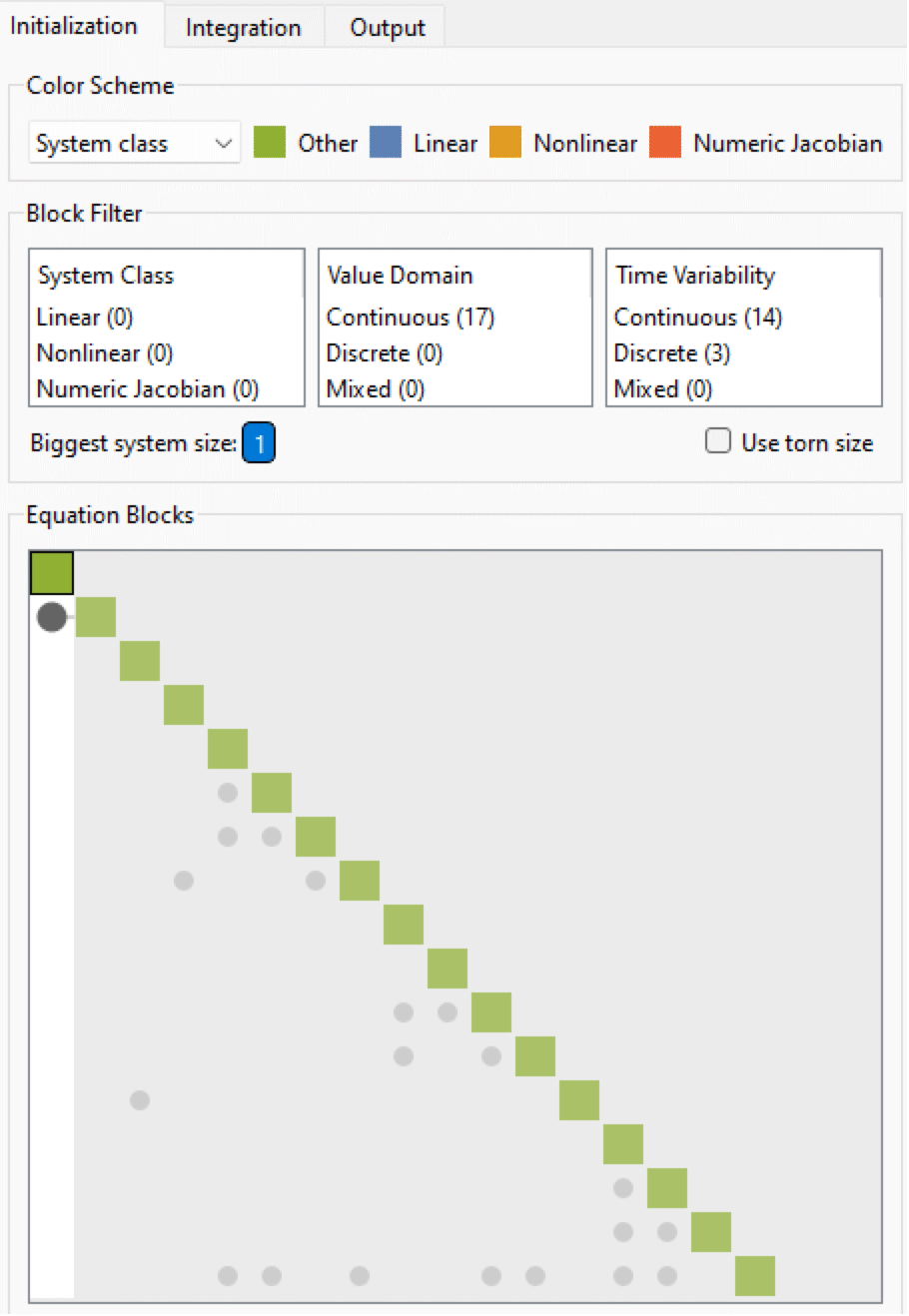
モデルが緑に戻ったので,Initializationタブでそのようなフィルタの追加による考えられる結果をさらに見てみよう.初期化問題が,すべて緑ではあるが,もはや以前ほど単純ではないことが分かるだろう.
Initializationタブにおけるモデルの方程式ブロック
さらに,先に見たstep成分からの純粋な階段とは対照的に出力信号が定値になる前に初期振動を示している.
まとめ
この単純な例は方程式ブラウザおよびその使い方の導入となっており,非線形ブロックを線形ブロックに単純に分割する方法が示してある.特に,フィルターを導入することで分割統治することが可能になっている.この小さな例では、フィルターを追加してもシミュレーションの実行時間に大きな違いはなかったため,モデルのパフォーマンスを調べる必要はなかった.
ループを分断して非線形ブロックを除去することは完全に費用がかからなかった訳ではない.こうするためには,(1)初期化問題を,まだ完全に線形ではあるが,若干複雑にせざるを得ず,(2)初期のシミュレーション時間ステップ中に出力信号にいくつかのアーティファクト(振動)が導入された.
この例では平衡状態つまり一定の値に達した後のシステムの応答にしか興味を抱かなかったが,場合によっては,このような初期化の変更とシステムの応答は望ましくないかもしれない.これには方程式ブラウザやブラインドショット等の解像度を利用しないように,Modelerを注意深く検査する必要がある.