WOLFRAM SYSTEM MODELER
FreeKickScenarioExample model with a soccer ball being kicked from a corner position. |
|
Diagram
Wolfram Language

SystemModel["EducationExamples.Physics.FreeKick.FreeKickScenario"]
Information
This model studies the physical effects acting on a soccer ball in flight.
Model
The example model consists of a ball being kicked. Gravity is affecting the ball and pulling it downward. A drag force, affecting the ball in the opposite direction of the velocity vector, will slow the ball down. The spin on the ball gives rise to a force, perpendicular to the spin axis and velocity vector. This force is called the Magnus force.
The drag and Magnus forces are visualized automatically in the simulation and can thus be examined in different scenarios. Change the initial velocity and rotational velocity to simulate different kicks.
Simulation
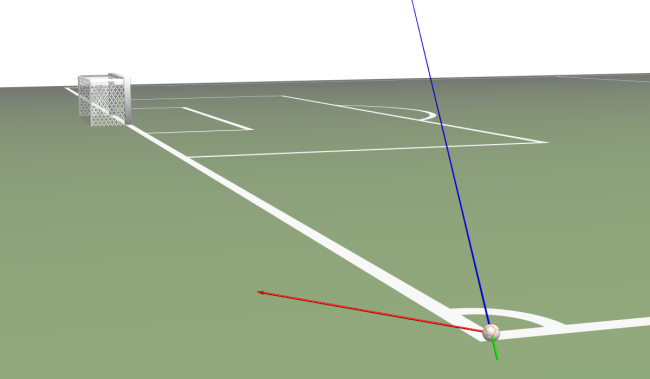
Simulating the model will give the possibility to look at an animation of the ball and to examine the forces acting on the ball, either in the animation or in plots.
To simulate the model and see the generated 3D animation, follow the steps below:
Click the Simulate button:
Click the Animation button:
Use your mouse or trackpad to drag the animation to a good angle and zoom in with your scroll wheel or by using the trackpad. Then click the Play button:
If the ball did not go as you wished, you can change the initial velocities and spin in Simulation Center and simulate again. Do this by opening the Parameters tab and expanding the ball tree. Change the corresponding initVel or initAngVel that you would like to change and then click the Simulate button:
To see exactly what the velocities or forces are, they can be plotted by opening the Plot tab and expanding the ball tree. Check the checkbox of the variable you want to analyze to plot it.
Further Investigation
If you would like to try another starting position of the ball, see the documentation for the Ball model.
The impact of the Magnus force can be seen in different scenarios by changing the initial angular velocity or the initial velocity, or by changing the object being thrown or kicked. In this example, we will limit ourselves to only using a soccer ball. The equations for the drag and Magnus forces are taken from the book Physics for Game Programmers (2005, Grant Palmer) and are stated as:
- FD = 1/2 ρ v^2 A CD
- FM = 1/2 ρ v^2 A CL
The tricky part is to calculate the drag coefficient (CL) and lift coefficient (CL). The other variables are air density (ρ), the cross-sectional area of the ball (A), and the velocity of the ball (v). The lift and drag coefficients are often measured in experiments for different angular velocities, the Reynolds number, and velocities. The results are then used to create a function that approximates both coefficients respectively.
Parameters (3)
| ballMass |
Value: 0.425 Type: Mass (kg) Description: Mass of the ball |
|---|---|
| ballRadius |
Value: 0.11 Type: Length (m) Description: Radius of the ball |
| temp |
Value: 293.15 Type: Temperature (K) Description: Temperature of the air |