WOLFRAM SYSTEM MODELER
InitSpringConstantDetermine spring constant such that system is in steady state at given position |
|
Diagram
Wolfram Language

SystemModel["Modelica.Mechanics.MultiBody.Examples.Elementary.InitSpringConstant"]
Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
This example demonstrates a non-standard type of initialization by calculating a spring constant such that a simple pendulum is at a defined position in steady state.
The goal is that the pendulum should be in steady state when the rotation angle of the pendulum is zero. The spring constant of the spring shall be calculated during initialization such that this goal is reached.
The pendulum has one degree of freedom, i.e., two states. Therefore, two additional equations have to be provided for initialization. However, parameter "c" of the spring component is defined with attribute "fixed = false", i.e., the value of this parameter is computed during initialization. Therefore, there is one additional equation required during initialization. The 3 initial equations are the rotational angle of the revolute joint and its first and second derivative. The latter ones are zero, in order to initialize in steady state. By setting the start values of phi, w, a to zero and their fixed attributes to true, the required 3 initial equations are defined.
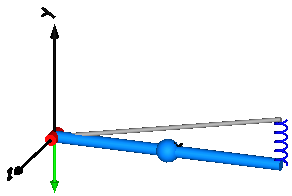
After translation, this model is initialized in steady-state. The spring constant is computed as c = 49.05 N/m. An animation of this simulation is shown in the figure below.
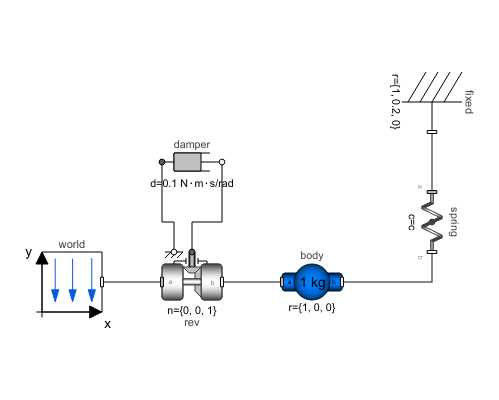
Components (6)
| world |
Type: World Description: World coordinate system + gravity field + default animation definition |
|
|---|---|---|
| rev |
Type: Revolute Description: Revolute joint (1 rotational degree-of-freedom, 2 potential states, optional axis flange) |
|
| damper |
Type: Damper Description: Linear 1D rotational damper |
|
| body |
Type: BodyShape Description: Rigid body with mass, inertia tensor, different shapes for animation, and two frame connectors (12 potential states) |
|
| fixed |
Type: Fixed Description: Frame fixed in the world frame at a given position |
|
| spring |
Type: Spring Description: Linear translational spring with optional mass |