WOLFRAM SYSTEM MODELER
Fourbar_analyticOne kinematic loop with four bars (with JointSSP joint; analytic solution of non-linear algebraic loop) |
|
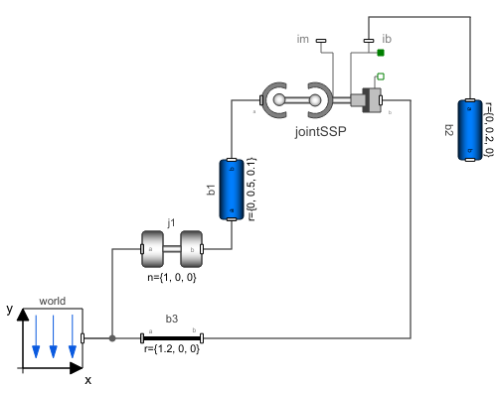
Diagram
Wolfram Language

SystemModel["Modelica.Mechanics.MultiBody.Examples.Loops.Fourbar_analytic"]
Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
This is a third version of the "four-bar" mechanism, see figure:
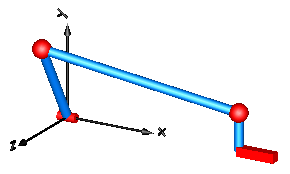
In this case the three revolute joints on the left top-side and the two revolute joints on the right top side have been replaced by the assembly joint Joints.Assemblies.JointSSP which consists of two spherical joints and one prismatic joint. Since JointSSP solves the non-linear constraint equation internally analytically, no non-linear equation appears any more and a Modelica translator can transform the system into state space form without solving a system of equations. For more details, see MultiBody.UsersGuide.Tutorial.LoopStructures.AnalyticLoopHandling.
Outputs (4)
| j1_phi |
Type: Angle (rad) Description: Angle of revolute joint j1 |
|---|---|
| j2_s |
Type: Position (m) Description: Distance of prismatic joint j2 |
| j1_w |
Type: AngularVelocity (rad/s) Description: Axis speed of revolute joint j1 |
| j2_v |
Type: Velocity (m/s) Description: Axis velocity of prismatic joint j2 |
Components (6)
| world |
Type: World Description: World coordinate system + gravity field + default animation definition |
|
|---|---|---|
| j1 |
Type: Revolute Description: Revolute joint (1 rotational degree-of-freedom, 2 potential states, optional axis flange) |
|
| b1 |
Type: BodyCylinder Description: Rigid body with cylinder shape. Mass and animation properties are computed from cylinder data and density (12 potential states) |
|
| b3 |
Type: FixedTranslation Description: Fixed translation of frame_b with respect to frame_a |
|
| jointSSP |
Type: JointSSP Description: Spherical - spherical - prismatic joint aggregation with mass (no constraints, no potential states) |
|
| b2 |
Type: BodyCylinder Description: Rigid body with cylinder shape. Mass and animation properties are computed from cylinder data and density (12 potential states) |