WOLFRAM SYSTEM MODELER
VoluminousWheelVisualizing a voluminous wheel |
|
Diagram
Wolfram Language

SystemModel["Modelica.Mechanics.MultiBody.Visualizers.VoluminousWheel"]

Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
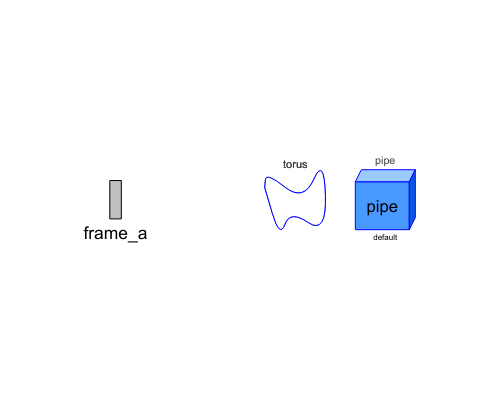
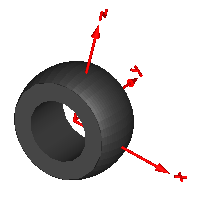
Model VoluminousWheel provides a simple visualization of a tire using a torus and a pipe shape object. The center of the wheel is located at connector frame_a (visualized by the red coordinate system in the figure below).
Parameters (9)
| animation |
Value: true Type: Boolean Description: = true, if animation shall be enabled |
|---|---|
| rTire |
Value: 0.25 Type: Radius (m) Description: Radius of the tire |
| rRim |
Value: 0.14 Type: Radius (m) Description: Radius of the rim |
| width |
Value: 0.25 Type: Radius (m) Description: Width of the tire |
| rCurvature |
Value: 0.30 Type: Radius (m) Description: Radius of the tire's cross section |
| color |
Value: {64, 64, 64} Type: RealColor Description: Color of tire |
| specularCoefficient |
Value: 0.5 Type: SpecularCoefficient Description: Reflection of ambient light (= 0: light is completely absorbed) |
| n_rTire |
Value: 40 Type: Integer Description: Number of points along rTire |
| n_rCurvature |
Value: 20 Type: Integer Description: Number of points along rCurvature |
Connectors (1)
| frame_a |
Type: Frame_a Description: Coordinate system in which visualization data is resolved |
|---|
Components (3)
| world |
Type: World Description: World coordinate system + gravity field + default animation definition |
|
|---|---|---|
| pipe |
Type: Shape Description: Visualizing an elementary object with variable size; all data have to be set as modifiers (see info layer) |
|
| torus |
Type: Surface Description: Visualizing a moveable, parameterized surface; the surface characteristic is provided by a function |
Revisions
- July 2010 by Martin Otter
Adapted to the new Surface model. - July 2005 by Dirk Zimmer (practical training at DLR)
First version to visualize a multi-level tyre wheel model.