Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

FindFormula

FindFormula[data]

finds a pure function that approximates data.

FindFormula[data,x]

finds a symbolic function of the variable x that approximates data.

FindFormula[data,x,n]

finds up to n functions that approximate data.

FindFormula[data,x,n,prop]

returns up to n best functions associated with property prop.

FindFormula[data,x,n,{prop₁,prop₂,…}]

returns up to n best functions associated with properties prop₁, prop₂, etc.

Details and Options

The data should be either an array of the form {{x₁,y₁},{x₂,y₂},…} or {y₁,y₂,…}, or a TimeSeries object.
Data of the form {y₁,y₂,…} is equivalent to data of the form {{1,y₁},{2,y₂},…}.
FindFormula[data,x,n,All] creates a Dataset object with all possible properties.
Properties supported include:
"Score" internal score

"Complexity" complexity of the function

"Error" mean squared error

All all the previous properties
The following options can be given:

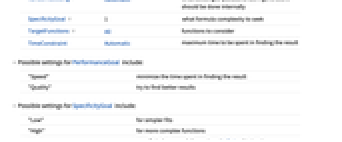
	PerformanceGoal	Automatic	aspect of performance to optimize
	RandomSeeding	Automatic	what seeding of pseudorandom generators should be done internally
	SpecificityGoal	1	what formula complexity to seek
	TargetFunctions	All	functions to consider
	TimeConstraint	Automatic	maximum time to be spent in finding the result

Possible settings for PerformanceGoal include:
"Speed" minimize the time spent in finding the result

"Quality" try to find better results
Possible settings for SpecificityGoal include:
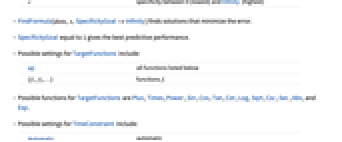
"Low" for simpler fits

"High" for more complex functions

s specificity between 0 (lowest) and Infinity (highest)
FindFormula[data,x,SpecificityGoal->Infinity] finds solutions that minimize the error.
SpecificityGoal equal to 1 gives the best predictive performance.
Possible settings for TargetFunctions include:
All all functions listed below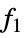

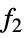{,,…} functions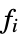
Possible functions for TargetFunctions are Plus, Times, Power, Sin, Cos, Tan, Cot, Log, Sqrt, Csc, Sec, Abs, and Exp.
Possible settings for TimeConstraint include:
Automatic automatic

t maximum t seconds
Possible settings for RandomSeeding include:

	Automatic	automatically reseed every time the function is called
	Inherited	use externally seeded random numbers
	seed	use an explicit integer or strings as a seed

Examples

open allclose all

Basic Examples (2)

Make a table of values of the function x Sin[x]:

FindFormula finds a formula that generates the data:

Plot the exponents of known Mersenne primes:

Find the best simple function describing the data:

Visualize the fitted functions with the data:

Scope (3)

Generate data with normally distributed noise:

Visualize the data:

Find the first 5 best functions that approximate data:

Visualize the fitted functions with the data:

Generate data with normally distributed noise:

Visualize the data:

Visualize the dataset for the first 5 functions that approximate data:

Generate data with normally distributed noise:

Visualize the data:

Look at the first 300 fits and plot their score as functions of the errors and complexity for different settings of SpecificityGoal:

Visualize the first fitted function with the data:

Options (4)

PerformanceGoal (1)

Generate data with normally distributed noise:

Visualize the data:

Find the best function that approximates data with its internal score:

Find the best function that approximates data using PerformanceGoal with its internal score:

Visualize the fitted functions with the data:

RandomSeeding (1)

Generate data with normally distributed noise:

Compare different evaluations of FindFormula and notice how they differ:

Use the option RandomSeeding to avoid having different results:

SpecificityGoal (1)

Generate data with normally distributed noise:

Visualize the data:

Find the best functions that approximate data with their errors using different values of SpecificityGoal:

Visualize the fitted functions with the data:

TargetFunctions (1)

Generate data with normally distributed noise:

Visualize the data:

Find the best function that approximates data:

Find the best function that approximates data using TargetFunctions:

Visualize the fitted functions with the data:

Applications (3)

Population Growth (1)

Population growth in Poland:

Find the best function that describes data:

Visualize the fitted function with the data:

Find a fit for the first 100 prime numbers:

Compare the fit with the data and with the next 200 primes:

Differential Equation (1)

Find a fit for the numerical solution of a differential equation:

Compare the fit with the data:

Orbital Mechanics (1)

Plot the orbital periods of planets vs. their semimajor axes:

Find the best simple function describing the orbital radius in terms of the orbital period:

Find the constant of proportionality:

Compare with the exact formula given by Kepler's third law:

The exact constant of proportionality has value:

Compare with the different values from the orbital data directly:

Top