FindDistribution
FindDistribution[data]
finds a simple functional form to fit the distribution of data.
FindDistribution[data,n]
finds up to n best distributions.
FindDistribution[data,n,prop]
returns up to n best distributions associated with property prop.
FindDistribution[data,n,{prop1,prop2,…}]
returns up to n best distributions associated with properties prop1, prop2, etc.
Details and Options
- The data must be a list of possible outcomes from a univariate distribution.
- FindDistribution[data,n,All] creates a Dataset object with all possible properties.
- Properties supported include:
-
"BIC" Bayesian information criterion "AIC" Akaike information criterion "HQIC" Hannan–Quinn information criterion "Score" internal score "Complexity" complexity of the distribution "LogLikelihood" LogLikelihood value "PearsonChiSquare" PearsonChiSquareTest p-value "CramerVonMises" CramerVonMisesTest p-value All all the previous properties - The following options can be given:
-
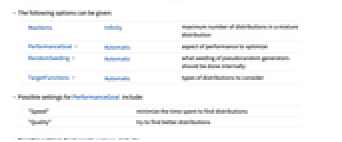
MaxItems Infinity maximum number of distributions in a mixture distribution PerformanceGoal Automatic aspect of performance to optimize RandomSeeding Automatic what seeding of pseudorandom generators should be done internally TargetFunctions Automatic types of distributions to consider - Possible settings for PerformanceGoal include:
-
"Speed" minimize the time spent to find distributions "Quality" try to find better distributions - Possible settings for TargetFunctions include:
-
Automatic automatically chosen distributions All all built-in distributions "Continuous" all continuous distributions "Discrete" all discrete distributions {dist1,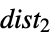 
,
}distributions disti {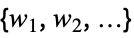 
{dist1,
,
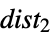}}distributions disti using weights wi - Possible settings for RandomSeeding include:
-
Automatic automatically reseed every time the function is called Inherited use externally seeded random numbers seed use an explicit integer or strings as a seed - Possible continuous distributions for TargetFunctions are: BetaDistribution, CauchyDistribution, ChiDistribution, ChiSquareDistribution, ExponentialDistribution, ExtremeValueDistribution, FrechetDistribution, GammaDistribution, GumbelDistribution, HalfNormalDistribution, InverseGaussianDistribution, LaplaceDistribution, LevyDistribution, LogisticDistribution, LogNormalDistribution, MaxwellDistribution, NormalDistribution, ParetoDistribution, RayleighDistribution, StudentTDistribution, UniformDistribution, WeibullDistribution, HistogramDistribution.
- Possible discrete distributions for TargetFunctions are: BenfordDistribution, BinomialDistribution, BorelTannerDistribution, DiscreteUniformDistribution, GeometricDistribution, LogSeriesDistribution, NegativeBinomialDistribution, PascalDistribution, PoissonDistribution, WaringYuleDistribution, ZipfDistribution, HistogramDistribution, EmpiricalDistribution.
- The internal information criterion uses a Bayesian information criterion together with priors over TargetFunctions.
Examples
open allclose allBasic Examples (2)
Create a list of uniformly distributed random integers:
Find the underlying distribution from the data:
Generate data sampled from an exponential distribution:
| In[1]:= |
Find the best distribution from the data:
Compare the PDFs for the original and estimated distributions:
Return the best three distributions:
Compare their Bayesian information criterion and Akaike information criterion values:
Scope (3)
Options (5)
Applications (5)
Properties & Relations (1)
See Also
FindDistributionParameters DistributionFitTest Likelihood EstimatedDistribution EmpiricalDistribution SmoothKernelDistribution FindFormula