Fourier

Fourier[list]

finds the discrete Fourier transform of a list of complex numbers.

Fourier[list,{p1,p2,…}]

returns the specified positions of the discrete Fourier transform.

Details and Options

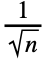
  • The discrete Fourier transform vs of a list ur of length n is by default defined to be 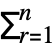ure2π i(r-1)(s-1)/n. »
  • Note that the zero frequency term appears at position 1 in the resulting list.
  • Other definitions are used in some scientific and technical fields.
  • Different choices of definitions can be specified using the option FourierParameters.
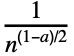
  • With the setting FourierParameters->{a,b}, the discrete Fourier transform computed by Fourier is 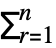ure2π i b(r-1)(s-1)/n. »
  • Some common choices for {a,b} are {0,1} (default), {-1,1} (data analysis), {1,-1} (signal processing).
  • The setting 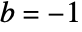effectively corresponds to conjugating both input and output lists.
  • To ensure a unique inverse discrete Fourier transform, b must be relatively prime to n. »
  • The list of data supplied to Fourier need not have a length equal to a power of two.
  • The list given in Fourier[list] can be nested to represent an array of data in any number of dimensions.
  • The array of data must be rectangular.
  • If the elements of list are exact numbers, Fourier begins by applying N to them.
  • Fourier[list,{p1,p2,…}] is typically equivalent to Extract[Fourier[list],{p1,p2,…}]. Cases with just a few positions p are computed using an algorithm that takes less time and memory but is more subject to numerical error, particularly when the length of list is long.
  • Fourier can be used on SparseArray objects.

Examples

open allclose all

Basic Examples  (2)

Find a discrete Fourier transform:

Find a power spectrum:

Scope  (3)

x is a list of real values:

Compute the Fourier transform with machine arithmetic:

Compute using 24-digit precision arithmetic:

Compute a 2D Fourier transform:

x is a rank 3 tensor with nonzero diagonal:

Compute the 3D Fourier transform:

Options  (2)

FourierParameters  (2)

No normalization:

Normalization by :

Normalization by :

Data from a Sinc function with noise:

Ordinary spectrum without normalization:

Partial spectrum:

Applications  (10)

Computing Spectra  (6)

Fourier spectrum of "white noise":

Show the logarithmic spectrum, including the first (DC) component:

The spectrum of a "pulse" is completely flat:

Power spectrum of the Thue–Morse nested sequence [more info]:

Power spectrum of the Fibonacci nested sequence [more info]:

2D power spectrum of a nested pattern:

Plot the nested pattern:

Find the logarithmic power spectrum:

Find the Fourier transform of the rule 30 cellular automaton pattern:

Logarithmic power spectrum:

Filtering Data  (1)

Compute discrete cyclic convolutions to smooth a discontinuous function with a Gaussian:

Compute the cyclic convolution:

Show the original and smoothed function:

The convolution is consistent with ListConvolve:

Frequency Identification  (1)

Here is some periodic data with some noise:

Find the maximum modes in the spectrum:

Get the position corresponding to positive frequencies and show the position on a plot of the spectrum:

Find a high-resolution spectrum between modes where the maximum was found:

Determine the period from the frequencies:

Computing Eigenvectors  (1)

m is a circulant differentiation matrix:

Because , the eigenvalues of m are:

The eigenvectors are the columns of the DFT matrix, so Fourier diagonalizes m:

This allows very efficient computation of MatrixExp[m,r] for a particular vector:

Show the approximate evolution of the heat equation on the unit interval:

Fractional Fourier Transform  (1)

Define a fractional Fourier transform using different choices of FourierParameters:

Properties & Relations  (6)

InverseFourier inverts Fourier:

For real inputs, all elements after the first come in complex conjugate pairs:

The power spectrum is symmetric:

Cyclic convolution corresponds to multiplication of Fourier transforms:

is given by :

Fourier is equivalent to multiplication with FourierMatrix:

The conjugate transpose of the matrix is equivalent to InverseFourier:

Possible Issues  (4)

If is not relatively prime to , the transform may not be invertible:

Lengths that are powers of 2 or factorizable into a product of small primes will be faster:

Fourier uses an efficient algorithm when only a small number of coefficients is needed:

The fast and efficient implementation may result in significant numerical error:

Wolfram Research (1988), Fourier, Wolfram Language function, https://reference.wolfram.com/language/ref/Fourier.html (updated 2012).

Text

Wolfram Research (1988), Fourier, Wolfram Language function, https://reference.wolfram.com/language/ref/Fourier.html (updated 2012).

CMS

Wolfram Language. 1988. "Fourier." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2012. https://reference.wolfram.com/language/ref/Fourier.html.

APA

Wolfram Language. (1988). Fourier. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Fourier.html

BibTeX

@misc{reference.wolfram_2024_fourier, author="Wolfram Research", title="{Fourier}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/Fourier.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fourier, organization={Wolfram Research}, title={Fourier}, year={2012}, url={https://reference.wolfram.com/language/ref/Fourier.html}, note=[Accessed: 14-November-2024 ]}