Input Syntax
Input Syntax
■
Enter it directly (e.g.
+
)
|
■
Enter it by full name (e.g.
∖[Alpha]
)
|
■
Enter it by alias (e.g.
Esc
a
Esc
) (notebook front end only)
|
■
Enter it by choosing from a palette (notebook front end only)
|
■
Enter it by character code (e.g.
∖:03b1
)
|
All printable ASCII characters can be entered directly. Those that are not alphanumeric are assigned explicit names in the Wolfram Language, allowing them to be entered even on keyboards where they do not explicitly appear.
|
|
All characters which are entered into the Wolfram Language kernel are interpreted according to the setting for the CharacterEncoding option for the stream from which they came.
| ∖[Name] | a character with the specified full name |
| ∖nnn | a character with octal code nnn |
| ∖.nn | a character with hexadecimal code nn |
| ∖:nnnn | a character with hexadecimal code nnnn |
| ∖|nnnnnn | a character with hexadecimal code nnnnnn |
Codes for characters can be generated using ToCharacterCode. The Unicode standard is followed, with various extensions.
8‐bit characters have codes less than 256; 16‐bit characters have codes between 256 and 65535; all characters have codes less than 1114112. Approximately 1200 characters are assigned explicit names in the Wolfram Language. Other characters must be entered using their character codes.
| ∖∖ |
single backslash (decimal code 92)
|
| ∖ |
single space (decimal code 32)
|
| ∖ |
double quote (decimal code 34)
|
| ∖b | backspace or Ctrl+H (decimal code 8) |
| ∖t | tab or Ctrl+I (decimal code 9) |
| ∖n | newline or Ctrl+J (decimal code 10; full name ∖[NewLine]) |
| ∖f | form feed or Ctrl+L (decimal code 12) |
| ∖r | carriage return or Ctrl+M (decimal code 13) |
| ∖000 |
null byte (code 0)
|
The standard input syntax used by the Wolfram Language is the one used by default in InputForm and StandardForm. You can modify the syntax by making definitions for MakeExpression[expr,form].
Options can be set to specify what form of input should be accepted by a particular cell in a notebook or from a particular stream.
The input syntax in TraditionalForm, for example, is different from that in InputForm and StandardForm.
In general, what input syntax does is to determine how a particular string or collection of boxes should be interpreted as an expression. When boxes are set up, say with the notebook front end, there can be hidden InterpretationBox or TagBox objects which modify the interpretation of the boxes.
| "characters" | a character string |
∖"
| a literal " in a character string |
∖∖
| a literal ∖ in a character string |
∖
(at end of line)
| ignore the following newline |
∖!∖(…∖)
| a substring representing two‐dimensional boxes |
Character strings can contain any sequence of characters. Characters entered by name or character code are stored the same as if they were entered directly.
In a notebook front end, text pasted into a string by default automatically has appropriate ∖ characters inserted so that the string stored in the Wolfram Language reproduces the text that was pasted.
StringExpression objects can be used to represent strings that contain symbolic constructs, such as pattern elements.
| name | symbol name |
| `name | symbol name in current context |
| context`name | symbol name in specified context |
| context` | context name |
| context1`context2` | compound context name |
| `context` | context relative to the current context |
Symbol names and contexts can contain any characters that are treated by the Wolfram Language as letters or letter‐like forms. They can contain digits but cannot start with them. Contexts must end in a backquote `.
| digits | integer |
| digits.digits | approximate number |
| base^^digits | integer in specified base |
| base^^digits.digits | approximate number in specified base |
| mantissa*^n |
scientific notation (
mantissa
×
10n
)
|
| base^^mantissa*^n |
scientific notation in specified base (
mantissa
×
basen
)
|
| number` | machine‐precision approximate number |
| number`s | arbitrary‐precision number with precision |
| number``s | arbitrary‐precision number with accuracy |
Numbers can be entered with the notation base^^digits in any base from 2 to 36. The base itself is given in decimal. For bases larger than 10, additional digits are chosen from the letters a–z or A–Z. Upper‐ and lower‐case letters are equivalent for these purposes. Floating‐point numbers can be specified by including . in the digits sequence.
In scientific notation, mantissa can contain ` marks. The exponent n must always be an integer, specified in decimal.
In the form base^^number`s the precision s is given in decimal, but it gives the effective number of digits of precision in the specified base, not in base 10.
An approximate number x is taken to be machine precision if the number of digits given in it is Ceiling[$MachinePrecision+1] or fewer. If more digits are given, then x is taken to be an arbitrary‐precision number. The accuracy of x is taken to be the number of digits that appear to the right of the decimal point, while its precision is taken to be Log[10,Abs[x]]+Accuracy[x].
Bracketed objects use explicit left and right delimiters to indicate their extent. They can appear anywhere within Wolfram Language input, and can be nested in any way.
The delimiters in bracketed objects are matchfix operators. But since these delimiters explicitly enclose all operands, no precedence need be assigned to such operators.
Comments can be nested, and can continue for any number of lines. They can contain any 8‐ or 16‐bit characters.
| {e1,e2,…} | List[e1,e2,…] |
| <|e1,e2,…|> | Association[e1,e2,…] |
| e1,e2,… | Association[e1,e2,…] |
| 〈e1,e2,…〉 | AngleBracket[e1,e2,…] |
| ⌊expr⌋ | Floor[expr] |
| ⌈expr⌉ | Ceiling[expr] |
| e1,e2,… | BracketingBar[e1,e2,…] |
| e1,e2,… | DoubleBracketingBar[e1,e2,…] |
| ∖(input∖) | input or grouping of boxes |
{} is List[], a list with zero elements. Similarly, <||> is Association[], an association with zero values.
The character ∖[InvisibleComma] can be used interchangeably with ordinary commas; the only difference is that ∖[InvisibleComma] will not be displayed.
When the delimiters are special characters, it is a convention that they are named ∖[LeftName] and ∖[RightName].
∖(…∖) is used to enter boxes using one‐dimensional strings. Note that within the outermost ∖(…∖) in a piece of input the syntax used is slightly different from outside, as described in "Input of Boxes".
Bracketed objects with heads explicitly delimit all their operands except the head. A precedence must be assigned to define the extent of the head.
The precedence of h[e] is high enough that !h[e] is interpreted as Not[h[e]]. However, h_s[e] is interpreted as (h_s)[e].
In addition to bracketed expressions, the Wolfram Language has a large collection of infix, prefix and postfix operators. These include operators for mathematical operations, string processing, pattern matching, functional programming and more. A complete list with detailed precedence and associativity information can be found in Operator Input Forms.
|
|
Any array of expressions represented by a GridBox is interpreted as a list of lists. Even if the GridBox has only one row, the interpretation is still 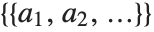 .
.
|
|
There is no issue of precedence for forms such as 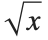 and
and  in which operands are effectively spanned by the operator. For forms such as
in which operands are effectively spanned by the operator. For forms such as  and
and  a left precedence does need to be specified, so such forms are included in the main table of precedences above.
a left precedence does need to be specified, so such forms are included in the main table of precedences above.
Control Keys
Ctrl+2 or Ctrl+@ | square root |
Ctrl+5 or Ctrl+% |
switch to alternate position (e.g. subscript to superscript)
|
Ctrl+6 or Ctrl+^ | superscript |
Ctrl+7 or Ctrl+& | overscript |
Ctrl+9 or Ctrl+( | begin a new cell within an existing cell |
Ctrl+0 or Ctrl+) | end a new cell within an existing cell |
Ctrl+- or Ctrl+_ | subscript |
Ctrl
+
Shift
+
,
| underscript |
Ctrl
+
Enter
| create a new row in a table |
Ctrl
+
,
| create a new column in a table |
Ctrl
+
.
| expand current selection |
Ctrl
+
/
| fraction |
Ctrl
+
Space
| return from current position or state |
Ctrl
+
←
,
Ctrl
+
→
,
Ctrl
+
↑
,
Ctrl
+
↓
| move an object by minimal increments on the screen |
On English‐language keyboards both forms will work where alternates are given. On other keyboards the first form should work but the second may not.
Boxes Constructed from Text
When textual input that you give is used to construct boxes, as in StandardForm or TraditionalForm cells in a notebook, the input is handled slightly differently from when it is fed directly to the kernel.
The input is broken into tokens, and then each token is included in the box structure as a separate character string. Thus, for example, xx+yyy is broken into the tokens "xx", "+", "yyy".
■
symbol name (e.g.
x123
)
|
■
number (e.g.
12.345
)
|
■
operator (e.g.
+=
)
|
■
spacing (e.g.
␣
)
|
■
character string (e.g.
"text"
)
|
A RowBox is constructed to hold each operator and its operands. The nesting of RowBox objects is determined by the precedence of the operators in standard Wolfram Language syntax.
Note that spacing characters are not automatically discarded. Instead, each sequence of consecutive such characters is made into a separate token.
String‐Based Input
Any textual input that you give between \( and \) is taken to specify boxes to construct. The boxes are only interpreted if you specify with \! that this should be done. Otherwise x\^y is left for example as SuperscriptBox[x,y], and is not converted to Power[x,y].
Within the outermost \(…∖), further \(…∖) specify grouping and lead to the insertion of RowBox objects.
| ∖(box1,box2,…∖) | RowBox[box1,box2,…] |
| box1∖^box2 | SuperscriptBox[box1,box2] |
| box1∖_box2 | SubscriptBox[box1,box2] |
| box1∖_box2∖%box3 | SubsuperscriptBox[box1,box2,box3] |
| box1∖&box2 | OverscriptBox[box1,box2] |
| box1∖+box2 | UnderscriptBox[box1,box2] |
| box1∖+box2∖%box3 | UnderoverscriptBox[box1,box2,box3] |
| box1∖/box2 | FractionBox[box1,box2] |
| \@box | SqrtBox[box] |
| form∖` box | FormBox[box,form] |
| \*input | construct box by interpreting input |
| \␣ | insert a space |
| \n | insert a newline |
| \t | indent at the beginning of a line |
In string‐based input between \( and \) spaces, tabs and newlines are discarded. ∖␣ can be used to insert a single space. Special spacing characters such as \[ThinSpace], \[ThickSpace], or \[NegativeThinSpace] are not discarded.
When you input typesetting forms into a string, the internal representation of the string uses the above forms. The front end displays the typeset form, but uses the \(…∖) notation when saving the content to a file or when sending the string to the kernel for evaluation.
The Wolfram Language will treat all input that you give on a single line as being part of the same expression.
The Wolfram Language allows a single expression to continue for several lines. In general, it treats the input that you give on successive lines as belonging to the same expression whenever no complete expression would be formed without doing this.
Thus, for example, if one line ends with =, then the Wolfram Language will assume that the expression must continue on the next line. It will do the same if for example parentheses or other matchfix operators remain open at the end of the line.
If at the end of a particular line the input you have given so far corresponds to a complete expression, then the Wolfram Language will normally begin immediately to process that expression.
You can however explicitly tell the Wolfram Language that a particular expression is incomplete by putting a ∖ or a (\[Continuation]) at the end of the line. The Wolfram Language will then include the next line in the same expression, discarding any spaces or tabs that occur at the beginning of that line.
| ?symbol | get information |
| ??symbol | get more information |
| ?s1s2… | get information on several objects |
| ! command |
execute an external command (text-based interface only)
|
display the contents of an external file (text-based interface only)
|
In most implementations of the Wolfram Language, you can give a line of special input anywhere in your input. The only constraint is that the special input must start at the beginning of a line.
Some implementations of the Wolfram Language may not allow you to execute external commands using !command.
Notebook files as well as front end initialization files can contain a subset of standard Wolfram Language syntax. This syntax includes:
- Any Wolfram Language expression in FullForm.
- Lists in {…} form. The operators ->, :>, and &. Function slots in # form.
- Various Wolfram Language operators such as +, *, ;, etc.
- Special characters in ∖[Name], ∖:nnnn, or ∖.xx form.
- String representation of boxes involving ∖(, ∖), and other backslash operators.
- Wolfram Language comments delimited by (* and *).