Many modern control techniques, such as the H-infinity robustness methodology, require the system model to be put into the form of a coprime matrix fraction representation. Functions to generate left and right matrix-fraction models have been implemented in Polynomial Control Systems (see Section 3.4.1 and Section 3.4.2). This generates a right matrix-fraction model of the distillation column. | Out[2]= | 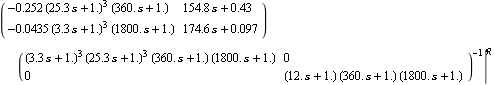 |
This is a left matrix-fraction model of the same system. | Out[4]= | 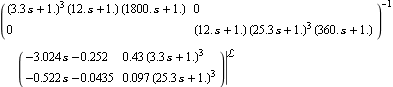 |
The denominator and numerator matrices in this left matrix-fraction model are coprime (see Section 4.3.1). | Out[6]= | 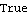 |
There are many system matrix models that correspond to the same transfer-function matrix. Given a TransferFunction model as input, SystemMatrix, by default, constructs the right matrix-fraction form of the system matrix in polynomial form (see Section 3.3.1). Here is an initial 11th-order system matrix model of the distillation column in polynomial form. | Out[8]= | 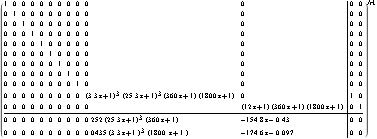 |
For the application of modern synthesis techniques, such as pole assignment using state or output feedback, the designer usually needs a state-space form of the system model in which, for the use of state feedback, the system must be completely controllable and, for the use of output feedback, the system must be both completely observable and completely controllable. Here is a previously developed state-space model of the distillation column, with 11 states. NumberForm displays a smaller sized output. | Out[11]= |  |
The state-space model is controllable, but not observable. | Out[13]= |  |
| Out[15]= |  |
There must be a total of two unobservable modes, because the McMillan degree, which is the total number of poles in the McMillan form of the transfer-function matrix model, indicates that a minimal state-space realization will only be of order 9 (see Section 4.1.3). | Out[17]= | 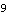 |
Given a StateSpace system as input, SystemMatrix produces a system matrix model in the state-space form (see Section 3.3.2). | Out[20]= | 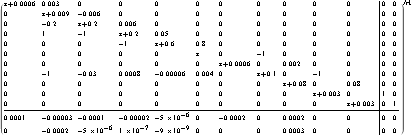 |
In the same way that state-space models can have uncontrollable modes and unobservable modes, system matrix models may have input decoupling zeros and output decoupling zeros, respectively (see Section 4.4.1). This determines the output decoupling zeros, or unobservable modes, of the system. | Out[22]= | 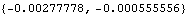 |
This removes the decoupling zeros and produces a least-order, or minimal, system matrix model of the distillation column in state-space form, which is of order 9 as expected (see Section 4.4.3). | Out[25]= | 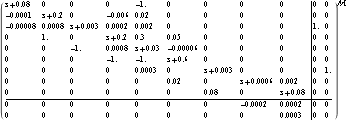 |
You can apply the tests for controllability and observability from Control System Professional directly to a system matrix model. | Out[27]= | 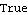 |
| Out[29]= |  |
|