NDSolve`FEM`
NDSolve`FEM`

ToBoundaryMesh

ToBoundaryMesh[r]

境界のElementMeshオブジェクトを領域 r の境界から生成する．

ToBoundaryMesh[r,{{xmin,xmax},…}]

境界ボックス[x_(min),x_(max)]x...に制約された領域 r の境界から境界のElementMeshオブジェクトを生成する．

ToBoundaryMesh[rules]

座標と境界要素を指定する rules の集合から境界のElementMeshオブジェクトを生成する．

ToBoundaryMesh[emesh]

既存のElementMesh，MeshRegion，BoundaryMeshRegionのいずれかから，新しい境界のElementMeshオブジェクトを生成する．

詳細とオプション

  • ToBoundaryMesh[r]は，記号的である可能性のある領域 r の境界を近似する境界のElementMeshオブジェクトを生成する．境界ElementMeshでは，"MeshElements"はAutomaticに設定され，ToElementMeshを使って計算することができる．
  • 領域の指定には，幾何学領域とImplicitRegionによって説明されるオブジェクトを含む．
  • 領域 r は，ConstantRegionQがTrueを与える定数領域でなければならない．
  • ToBoundaryMesh[rules]では，rules は以下の順序で与えられなければならない．
  • "Coordinates"->{c1,c2,…}座標が c1，c2，…になるように指定する必要がある
    "BoundaryElements"->{b1,…}メッシュの境界要素が b1，…になるように指定する必要がある
    "PointElements"->{p1,…}メッシュの点要素が p1，…になるように指定する（必須ではない）
  • 1D境界要素メッシュでは，"BoundaryElements"はPointElementである．
  • 2D境界要素メッシュでは，"BoundaryElements"はLineElementである．
  • 3D境界要素メッシュでは，"BoundaryElements"はTriangleElementでもQuadElementでもよい．
  • ToBoundaryMesh[emesh]を使って，さまざまな方法で，境界の抽出やマーカーの追加も含めて，ElementMeshオブジェクトemesh を修正することができる．
  • ToBoundaryMeshには次のオプションがある．
  • AccuracyGoalInfinity目標確度の桁数
    "BoundaryGroupingThreshold"Automatic法線の方向で境界のグループ分けを制御する
    "BoundaryMarkerFunction" None境界要素のマーカーを計算する関数
    "BoundaryMeshGenerator" Automatic境界のElementMeshを生成する関数
    "CheckIntersections"Automatic交差する境界の検定を制御する
    "DeleteDuplicateCoordinates" True重複する座標を削除する
    "IncludePoints" {}境界の一部として含まれ，考慮される点
    "MaxBoundaryCellMeasure" Automatic境界要素のサイズを制御する
    MaxCellMeasureAutomaticメッシュ要素のサイズを制御する
    "MeshOrder" Automatic要素メッシュの次数
    "MessageHead"Automaticメッセージ用のシンボル
    "PointMarkerFunction" None点要素のマーカーを計算する関数
    PrecisionGoalAutomatic目標精度の桁数
    "RegionHoles" Automatic領域の穴を指定する
  • MaxCellMeasure->m では，領域次元 d で作成されたセルの大きさは最高でも m である．d-1次元の境界表現セルの大きさは，デフォルトで大きさが m の高品質の d 次元のセルと互換性があるものが選ばれる．特定次元の限度は，MaxCellMeasure->{"Volume"->v,"Area"->a,"Length"->l}を使って指定することができる．
  • AccuracyGoal->a と PrecisionGoal->p では，領域 r あるいは離散化された領域 dreg と，RegionSymmetricDifference[r,dreg]内の任意の点との間の最大距離が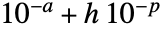，より小さくなるように保とうとされる．この場合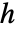， は境界ボックスの対角の長さである．
  • オプションの1つをToBoundaryMeshに指定することで，さまざまな方法で，ToBoundaryMesh[bmesh,opts]あるいはToBoundaryMesh[emesh,opts]を使って，境界のElementMeshオブジェクト bmesh を修正するか，完全なElementMeshオブジェクト emesh から境界を抽出するかすることができる．
  • ToBoundaryMeshがElementMeshを生成できない場合には，$Failedが返される．
  • EmptyRegionに対してToBoundaryMeshを呼び出すと，EmptyRegionが返される．
  • ToBoundaryMeshに与えられるオプションは，"MeshOptions"を指定することによってNDSolveに与えることができる． »
  • NDSolveおよび関連の関数からToBoundaryMeshのオプションを設定することについては，有限要素のためのNDSolveオプションに説明がある．

例題

すべて開くすべて閉じる

例  (4)

パッケージをロードする：

Diskの境界要素メッシュを作成する：

境界メッシュを可視化する：

境界要素メッシュを完全なメッシュに変換する：

DiskとRectangleの和集合の境界メッシュを作成する：

境界メッシュを可視化する：

明示的に境界要素を指定することによって境界メッシュを作成する：

境界メッシュを可視化する：

境界メッシュから完全な要素メッシュを作成し，結果の要素メッシュを可視化する：

円柱の離散化された境界表現を得る：

スコープ  (15)

Diskの境界メッシュを生成する：

ImplicitRegionを明示的な境界ボックスで変換する：

GraphicsComplexを境界要素メッシュに変換する：

TransformedRegionを境界要素メッシュに変換する：

3DのBallを境界要素メッシュに変換する：

3DのGraphicsComplexを境界要素メッシュに変換する：

3DのTransformedRegionを境界要素メッシュに変換する：

境界要素メッシュを，4つの座標と1つの境界要素から作成する：

点集合については，ToBoundaryMeshは凸包を返す：

1Dの点要素の境界メッシュ  (2)

点要素の境界メッシュを作成する：

1Dの境界メッシュを暗黙領域から作成する：

2Dの線分要素の境界メッシュ  (1)

領域の中に追加のノードがある，線分要素の境界メッシュを作成する：

2Dの高次の境界要素メッシュ  (1)

二次の境界要素メッシュを作成する：

境界マーカー  (1)

境界マーカーは，領域境界上でNeumannValueを指定するのに便利であり，「要素メッシュの生成」の「マーカー」セクションに詳しく説明されている．

境界要素マーカーと領域内に1つの追加のノードを含んだ矩形を作成する：

境界メッシュを作成する：

境界メッシュとマーカーを可視化する：

点マーカー  (1)

点マーカーは，領域境界上でDirichletConditionを指定するのに便利であり，「要素メッシュの生成」の「マーカー」セクションに詳しく説明されている．

マーカー付きの境界要素と点要素，および領域内に1つの追加のノードを含む矩形を作成する：

境界メッシュを作成する：

ノード番号を青で，マーカーを赤で示し，境界メッシュ内の点要素を可視化する：

オプション  (27)

"AccuracyGoal"  (1)

離散化された境界表現が境界に近いものになるようにする：

境界の弧の重心を計算するヘルパ関数：

真の円板からの最大偏差は，弧の中心にある：

目標確度を大きくすると，より多くの点を使うことによってエラーが減る：

"BoundaryGroupingThreashold"  (7)

ToBoundaryMeshは，境界法線ベクトルを比べることによって，隣接する境界セグメントのグループに自動的にマーカーを割り当てる．

数値領域を作成する：

数値領域から境界メッシュを作成する：

現存の境界要素マーカーを調べる：

隣接する境界を可視化する：

要素マーカーが2または4である境界を可視化する：

現存する点の要素マーカーを調べる：

点マーカーを可視化する：

NDSolveValueでの境界条件を指定するために要素マーカーを使用する：

NeumannValueとPeriodicBoundaryConditionが境界要素マーカーを抽出するのに対し，DirichletConditionは点の要素マーカーを抽出する．

解を可視化する：

点の要素マーカー（赤）は，境界マーカー（青）から推測される．ノードの接続された境界要素マーカーが同じである場合には，ノードは同じマーカーを持つ．コーナー部分では，通常接続された境界マーカーは異なり，使用可能なマーカーに対して任意の選択がなされる：

どのマーカーがコーナーのノードに割り当てられるかを制御するために，"PointMarkerFunction"を指定することができる．次の例では，左側のノードはすべて2のマーカーになり，右側は4のマーカーになる．残りのマーカーは，自動的に計算されるものが使われる．

自動的に境界がグループ化されないようにする：

唯一の境界要素マーカーはデフォルトの0である：

自動の境界のグループ分けは，境界セグメントの法線を計算してから，隣接するセグメントのドット積を計算することにより，隣接する境界セグメントを選ぶ．ドット積が閾値 を超える場合，連続するセグメントは隣接していると見なされる．

閾値が である場合に境界要素がグループ分けされる粗い境界メッシュを作成する：

境界要素マーカーの和集合を調べる：

閾値が である場合に境界要素がグループ分けされる粗い境界メッシュを作成する：

境界要素マーカーの和集合を調べる：

1Dの境界メッシュを内部の境界とともに構築する：

境界要素には1.0（指数 (index 2）における内部境界が含まれる：

1Dでは，内部境界の境界法線は0であると見なされる：

境界要素マーカーの和集合を調べる：

離散化されたグラフィックスから3Dの境界要素メッシュを作成する：

数多くの境界グループについて色のリストを生成する：

要素マーカーが1である境界のみを可視化する：

異なる要素マーカーを持つ境界を調べる：

自動の境界のグループ分けは，数多くのグループを含む複雑な形状においても役に立つことがある．歯車を要素メッシュとしてインポートする：

境界メッシュと連続する境界グループを可視化する：

"BoundaryMarkerFunction"  (1)

境界マーカーは，領域境界上でNeumannValueを指定するのに便利であり，「要素メッシュの生成」の「マーカー」セクションに詳しく説明されている．

以下は，辺要素の座標によって，辺の整数マーカーを計算する関数である：

境界メッシュと境界マーカーを可視化する：

境界要素を調べる：

"PointElementMarkers"も計算された場合には，それらは，"BoundaryMarkerFunction"に与えられる関数の第2引数としてアクセス可能である：

"BoundaryMeshGenerator"  (8)

"Continuation"メソッドは，多くの場合にコーナー，尖点，急な変化をかなりうまく処理することができる曲線継続法を使う：

"RegionPlot"メソッドは，RegionPlotからの出力を改善することに基づいており，より速い場合もある：

"RegionPlot"メソッドは，境界メッシュの質を改善するサブオプションを持つ：

BoundaryDiscretizeRegionの境界メッシュ生成器にメソッドオプションを渡す：

範囲を指定する：

メソッドオプションをBoundaryDiscretizeRegionの境界メッシュ生成器に渡して，離散化アルゴリズムを細かく調整する：

境界メッシュをメッシュ範囲として可視化する：

"OpenCascade"の境界メッシュ生成器は，GraphicsまたはGraphics3Dのプリミティブからなる2Dまたは3DのBooleanRegion式を扱うのに大変適している．

領域を指定する：

"OpenCascade"を境界メッシュ生成器として使う：

境界メーカーの色を生成する：

境界マーカーをハイライトした，境界要素メッシュを可視化する：

"OpenCascade"の境界メッシュ生成器のオプションは以下の通りである：

境界メッシュ生成のオプションの詳細は，OpenCascadeLinkのチュートリアルの曲面メッシュについてのセクションに記載されている．

DiskとRectangleの結合体に"OpenCascade"の境界メッシュ生成器を使う：

境界メッシュを可視化する：

"OpenCascade"の境界メッシュ生成器は，内部境界と領域の穴を区別することができない：

境界メッシュを可視化する：

完全なメッシュが生成されると，領域全体にメッシュが掛けられる：

"RegionHoles"を設定することで，手作業で領域の穴を指定する：

完全なメッシュが領域の穴と材料の境界を認識するようになった：

複雑な形状については，デフォルトの境界メッシュ生成器を使うとよい．その場合には，内部境界は生成されないからである：

これでその境界メッシュの領域の穴を抽出できるようになった：

見付かった領域の穴は，"OpenCascade"の境界メッシュ生成器と一緒に使うことができる：

内部境界が存在する場合には，DirichletConditionあるいはNeumannValue等の境界条件を位置述語True と一緒に指定すると，これらの条件が内部境界に適用される．境界の特定の部分を指定するためには，より細かい境界述語を使うべきである．

内部境界メッシュ生成器を，カスタムメッシュ生成器に置き換える：

カスタムメッシュ生成器のオプションを指定する：

"DeleteDuplicateCoordinates"  (2)

一般に，重複する座標を持つメッシュは，メッシュ生成プロセスに予測がきかなくなるため，望ましくない．デフォルトで，重複する座標は削除される：

重複する座標が削除された場合には，要素のインシデントの指標は付け直されることがある：

"IncludePoints"  (1)

数値領域を作成する：

境界メッシュを調べる：

境界メッシュに追加する点を指定する：

境界メッシュに点を含める：

追加した点と一緒に境界メッシュを可視化する：

追加されたこれらの点は，境界の一部として見なされるが，実際の境界上にある必要はない．"IncludePoints"では，陰的な領域によって指定された境界上に追加の点を加えることはできないことに注意する．つまり，すべての"IncludePoints"のインスタンスは厳密に境界領域内になければならない．

数値領域から完全なメッシュを作成する：

"IncludePoints"を使って加えられた点は，DirichletConditionで使える．さらに，DirichletConditionの述部がTrueであれば，境界条件は加えられた点において有効となる．

"MaxBoundaryCellMeasure"  (2)

"MaxBoundaryCellMeasure"->m で境界セルの大きさが選ばれる：

境界セルとセルの大きさを指定する：

"MaxCellMeasure"  (2)

MaxCellMeasure->m で，セルの大きさが選ばれ，境界セルの大きさが埋込み次元内の高品質セルに適切なものに設定される：

特定の長さは，MaxCellMeasure->{"Length"->len}で指定することができる：

境界の弧の長さを計算するヘルパ関数：

これは，弧の最大長を返す：

境界メッシュから完全なメッシュを作成する：

"MeshOrder"  (1)

ToBoundaryMeshはデフォルトで一次境界メッシュを生成する：

メッシュ次数を調べる：

境界メッシュ上で積分し，積分の確度を求める：

二次境界メッシュを得るために，オプション"MeshOrder"を使うことができる：

メッシュ次数を調べる：

境界メッシュ上で積分し，積分の確度を求める：

"MeshOrder"オプションの詳細については，要素メッシュの生成と要素メッシュの可視化のチュートリアルを参照されたい．

"PointMarkerFunction"  (1)

点マーカーは，領域境界上でDirichletConditionを指定するのに便利であり，「要素メッシュの生成」の「マーカー」セクションに詳しく説明されている．

以下は，辺のノードの座標によって，点要素の整数マーカーを計算する関数である：

境界要素を調べる：

"RegionHoles"  (1)

内部領域を持つ境界メッシュを作成する：

境界メッシュから完全なメッシュを作成する：

内部領域と領域の穴の指定を含む境界メッシュを作成する：

境界メッシュの領域の穴を調べる：

境界メッシュから完全なメッシュを作成する：

アプリケーション  (1)

で2つのネストした半環帯の境界メッシュを生成する．それぞれの環帯は異なる部分領域を表す．1つ目の部分領域は内半径が で外半径が ，2つ目の部分領域は内半径が ，外半径が である．

まず3つの半円盤を作成し，次に3つの部分領域の和を生成し，最後に2つの環帯を作成するために最初の半円盤を穴とする．

1つ目の環帯の内半径と外半径を定義する：

2つ目の環帯の外半径を定義する：

Circleを使って半円盤を作成する：

半円盤の和が作成されると，左の境界は自動的に和から削除される．このため，領域をもう一度繋げるために，線分が作成され，半円盤の和に繋げられる．1つ目の半円盤に穴を開けるために，和を から まで，および から まで 方向に繋げ，1つ目の半円盤を脇にのける．

2つの線分を作成する：

半円盤と線分の和を生成する：

に限られた境界メッシュを生成する：

境界メッシュのワイヤフレームを可視化する：

特性と関係  (1)

ToBoundaryMeshのオプションをNDSolveに渡して，定常偏微分方程式を解く：

計算に使われたメッシュを可視化する：

考えられる問題  (6)

入力の記号的な領域に境界がなければ，デフォルトのからの境界ボックスが各空間方向に想定される：

明示的な境界ボックスを指定することによって，デフォルトが無効になる：

境界の特徴がうまく表示されないことがある：

境界要素の大きさを設定し，サンプル点を増やすとうまくいくかもしれない：

あるいは，"Continuation"の境界メッシュ生成器を使った方がうまくいくかもしれない：

指定された領域の境界上にある"IncludePoints"を指定することによって，完全なメッシュに変換することができない境界メッシュが作成されることがある：

指定された"IncludePoints"は，領域内部になければならない：

領域のどの程度内部に"IncludePoints"がなければならないかは，メッシュの曲率の確度によって異なる．

ToBoundaryMeshの引数は規則として指定し，正しい順序（"Coordinates"，"BoundaryElements"の順序で，次にオプショナルの規則"PointElements"を加える）で与えなければならない：

正しい順序で引数を指定する：

境界マーカーの自動割当ては，2つの境界要素に同じ境界マーカーが割り当てられているかどうかを見極める閾値に依存する．以下の境界メッシュについて考える：

境界マーカーが青，点のノード番号が赤のメッシュを可視化する：

ノード5とノード1，およびノード1とノード2の間の辺はどちらも境界マーカー1になっていることに注意する．オプション"BoundaryGroupingThreshold"を使うと，閾値を変更することができる：

もう一つの方法として，入力の際に予め境界マーカーを指定することもできる：

Wolfram Research (2014), ToBoundaryMesh, Wolfram言語関数， https://reference.wolfram.com/language/FEMDocumentation/ref/ToBoundaryMesh.html （2024年に更新）.

テキスト

Wolfram Research (2014), ToBoundaryMesh, Wolfram言語関数， https://reference.wolfram.com/language/FEMDocumentation/ref/ToBoundaryMesh.html （2024年に更新）.

CMS

Wolfram Language. 2014. "ToBoundaryMesh." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/FEMDocumentation/ref/ToBoundaryMesh.html.

APA

Wolfram Language. (2014). ToBoundaryMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FEMDocumentation/ref/ToBoundaryMesh.html

BibTeX

@misc{reference.wolfram_2024_toboundarymesh, author="Wolfram Research", title="{ToBoundaryMesh}", year="2024", howpublished="\url{https://reference.wolfram.com/language/FEMDocumentation/ref/ToBoundaryMesh.html}", note=[Accessed: 03-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_toboundarymesh, organization={Wolfram Research}, title={ToBoundaryMesh}, year={2024}, url={https://reference.wolfram.com/language/FEMDocumentation/ref/ToBoundaryMesh.html}, note=[Accessed: 03-December-2024 ]}