CommunityModularity
CommunityModularity[g,partition]
gives the community modularity of a partition.
CommunityModularity[g,assignment]
gives the community modularity of an assignment.
Details and Options
- CommunityModularity functionality is now available in the built-in Wolfram Language function GraphAssortativity.
- To use CommunityModularity, you first need to load the Graph Utilities Package using Needs["GraphUtilities`"].
- A community in a network is a group of vertices such that there is a higher density of edges within the group than between them.
- Given a graph
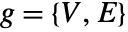, let the vertex set 
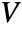be partitioned into 
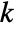subsets 
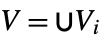such that each subset belongs to one community. The community modularity 
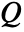of this partition is defined as
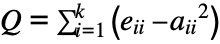, where 
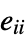is the percentage of edges that have both ends in community 
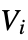, and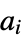 
is the percentage of edges that start from community 
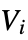. In other words,
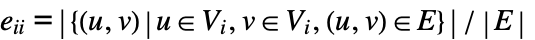and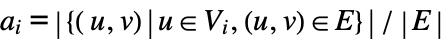 
. - The community modularity
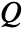is a number less than or equal to 1. A large positive value indicates that the vertex partition gives significant community structure. - The following option can be given:
-
Weighted False whether edges with higher weights are preferred during matching
Examples
open allclose allBasic Examples (2)
This gives the community modularity, assuming a partition {{1,2,3},{4,5,6}}:
CommunityModularity has been superseded by GraphAssortativity:
Options (1)
Weighted (1)
Text
Wolfram Research (2007), CommunityModularity, Wolfram Language function, https://reference.wolfram.com/language/GraphUtilities/ref/CommunityModularity.html.
CMS
Wolfram Language. 2007. "CommunityModularity." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/GraphUtilities/ref/CommunityModularity.html.
APA
Wolfram Language. (2007). CommunityModularity. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/GraphUtilities/ref/CommunityModularity.html