AASTriangle

AASTriangle[α,β,a]

角度が α および β で，辺の長さが a の塗り潰された三角形を返す．ただし，a は片方の角にのみ接している．

詳細とオプション

  • AASTriangleは，2つの角とその片方の角に接した辺が決まっている三角形である．
  • AASTriangleは，2Dグラフィックスではプリミティブとして，また2Dの幾何学領域として使うことができる．
  • AASTriangleの指定されたパラメータ（青）と計算されたパラメータ（赤）．
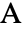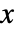  • AASTriangleは，原点に，正の 軸上に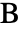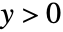，の半平面上に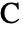があるTriangleを返す．
  • AASTriangleでは，長さ a は任意の正の数でよく，角度 α および β は α+β<π となるような正の数でよい．

予備知識

  • AASTriangleは，2つの角とその片方の角に接した辺が決まっている三角形を構築する．具体的に言うと，AASTriangle[α,β,a]は，頂点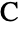，，が，順にTemplateBox[{}, Reals]^2上の，原点，正の 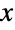軸上，上半平面に位置するTriangleを表す．α∠BAC，β∠ABCで，a は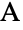の対辺の長さである．AAS定理により，このように指定された三角形は（幾何学的合同という点で）一意的である．AASTriangleの a の長さは任意の正の数でよく，角 α および角 β は α+β<π を満足する正の数でよい．AASTriangleの引数は厳密または近似の数式でよい．
  • AASTriangleが返すTriangleオブジェクトは，2Dのグラフィックスプリミティブあるいは幾何領域として使うことができる．
  • AASTriangleは数多くの他のシンボルと関連がある．ASATriangle，SASTriangle，SSSTriangleは，異なる角および／または辺の指定を使って構築された二次元の三角形を返す．最後に，AASTriangleは，AASTriangle[α,β,a]がTriangle[{{0,0},{a Csc[α] Sin[α+β],0},{a Cot[α] Sin[β],a Sin[β]}}]と等しいと言う意味で，Triangleの特殊ケースである．

例題

すべて開くすべて閉じる

例  (4)

，，の三角形：

AASTriangle：

異なるスタイルが適用されたAASTriangle：

面積と重心：

重心：

スコープ  (14)

グラフィックス  (4)

指定  (2)

AASTriangleを評価すると，原点に点の1つがあり，1辺が 軸上にあるTriangleになる：

記号による角度のある三角形：

プロットする：

スタイリング  (2)

面の色を色指示子で指定する：

FaceFormおよびEdgeFormを使って内側と境界のスタイルを指定することができる：

領域  (10)

埋込み次元は三角形がある空間の次元である：

幾何次元は三角形自体の次元である：

帰属判定：

帰属条件：

面積：

重心：

ある点からAASTriangleまでの距離：

これを可視化する：

点からの符号付きの距離：

最近点：

これを可視化する：

三角形は有界である：

その範囲を求める：

AASTriangle上で積分(Integrate)する：

この上で最適化する：

AASTriangle上で方程式を解く：

アプリケーション  (2)

2角が等しい三角形は，二等辺三角形である：

可視化する：

面積を求める：

AASTriangleの外接円は，Circumsphereを使って求めることができる：

外接円は3つの端点を通る：

三角形の各辺の中点を求める：

垂直二等分線は，外心から中点までの直線である：

特性と関係  (2)

AASTriangleはTriangleの特殊ケースである：

AASTriangleはPolygonで表すことができる：

おもしろい例題  (1)

角度を変える：

Wolfram Research (2014), AASTriangle, Wolfram言語関数， https://reference.wolfram.com/language/ref/AASTriangle.html.

テキスト

Wolfram Research (2014), AASTriangle, Wolfram言語関数， https://reference.wolfram.com/language/ref/AASTriangle.html.

CMS

Wolfram Language. 2014. "AASTriangle." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AASTriangle.html.

APA

Wolfram Language. (2014). AASTriangle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AASTriangle.html

BibTeX

@misc{reference.wolfram_2024_aastriangle, author="Wolfram Research", title="{AASTriangle}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/AASTriangle.html}", note=[Accessed: 30-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_aastriangle, organization={Wolfram Research}, title={AASTriangle}, year={2014}, url={https://reference.wolfram.com/language/ref/AASTriangle.html}, note=[Accessed: 30-December-2024 ]}